题目内容
11.已知BD为△ABC的角平分线,DE∥BC,交AB于点E,求证:$\frac{1}{AB}+\frac{1}{BC}=\frac{1}{DE}$.分析 先证明EB=ED,再根据平行线分线段成比例定理,由DE∥BC得到$\frac{DE}{BC}$=$\frac{AE}{AB}$,即$\frac{DE}{BC}$=$\frac{AB-BE}{AB}$,用等线段代换得到$\frac{DE}{BC}$=$\frac{AB-DE}{AB}$,然后根据比例的性质可得到结论.
解答 证明: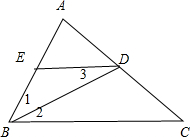 ∵BD为△ABC的角平分线,
∵BD为△ABC的角平分线,
∴∠1=∠2,
∵DE∥BC,
∴∠2=∠3,
∴EB=ED,
∴DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$,即$\frac{DE}{BC}$=$\frac{AB-BE}{AB}$,
∴$\frac{DE}{BC}$=$\frac{AB-DE}{AB}$,
∴$\frac{DE}{BC}$=1-$\frac{DE}{AB}$,
∴$\frac{1}{BC}$=$\frac{1}{DE}$-$\frac{1}{AB}$,
即$\frac{1}{AB}+\frac{1}{BC}=\frac{1}{DE}$.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.

练习册系列答案
相关题目
6.阅读材料:在△ABC中,有一点P,当P1、A、B、C没有任何三点在同一直线上,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互补重叠的小三角形的个数情况怎样?请观察图形和表格填空.表格中的空白处应填( )

| △ABC内点的个数 | 1 | 2 | 3 | … | 12 |
| 构成不重叠的小三角形的个数 | 3 | 5 | 7 | … |

| A. | 21 | B. | 23 | C. | 25 | D. | 28 |
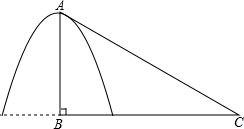 如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竿,它能否做帐篷的支撑竿,请说明理由.
如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竿,它能否做帐篷的支撑竿,请说明理由.