题目内容
2.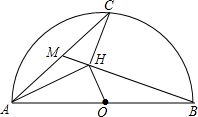 如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证:CH2=AH•OH.
如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证:CH2=AH•OH.
分析 连接OC、BC,可得∠BOC=∠BHC=90°,可得点O、B、C、H四点共圆,继而根据圆周角定理得出∠OHB=∠OCB=45°,然后证明△AMH∽△BMA,根据相似得出角相等,进而证得△AMH∽△BOH,最后根据相似三角形的性质证得结果.
解答 解:连接OC、BC,
∵C是弧AB的中点,M是弦AC的中点,
∴∠BOC=∠BHC=90°,
则点O、B、C、H四点共圆,
∴∠OHB=∠OCB=45°,
∵∠BCM=90°,CH⊥BM,M为AC的中点,
∴AM2=CM2=MH•MB,
即$\frac{HM}{AM}$=$\frac{AM}{BM}$,
∴△AMH∽△BMA,
则∠MAH=∠MBA,∠AHN=∠BAM=45°,
∴∠AHM=∠BHO,
∴△AMH∽△BOH,
∴$\frac{AH}{BH}$=$\frac{MH}{OH}$,
则AH•OH=MH•BH,
∵CH2=MH•HB,
∴CH2=AH•OH.
点评 本题考查了四点共圆的知识,涉及了相似三角形的判定与性质、圆周角定理以及射影定理等知识的运用,解答本题的关键是根据∠BOC=∠BHC=90°得出四点共圆,本题涉及知识点较多,比较复杂,难度适中.

练习册系列答案
相关题目
14.下列事件中,属于随机事件的是( )
| A. | 将油滴入水中,油会浮在水面 | |
| B. | 随意掷一枚均匀的骰子,掷出的点数是10 | |
| C. | 抛出的篮球会下落 | |
| D. | 任意买一张电影票,座位号是2的倍数 |
11.已知点P(a,b)是反比例函数y=$\frac{1}{x}$图象上异于点(-1,-1)的一个动点,则$\frac{1}{1+a}$+$\frac{1}{1+b}$=( )
| A. | 2 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
11.已知$\left\{\begin{array}{l}{x=2}\\{y=-2}\\{z=4}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax-\frac{1}{2}by+\frac{1}{4}cz=4}\\{\frac{1}{2}ax-by+\frac{1}{4}cz=2}\\{\frac{1}{2}ax-\frac{1}{2}by+\frac{1}{2}cz=6}\end{array}\right.$的解,则a,b,c的值( )
| A. | a=1,b=-1,c=3 | B. | a=-1,b=1,c=3 | C. | a=1,b=-1,c=-3 | D. | a=-1,b=1,c=-3 |
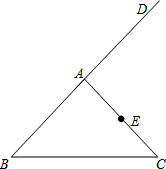 如图,在△ABC中,AB=AC,D是BA延长线上一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,点E是AC的中点.