题目内容
11.已知点P(a,b)是反比例函数y=$\frac{1}{x}$图象上异于点(-1,-1)的一个动点,则$\frac{1}{1+a}$+$\frac{1}{1+b}$=( )| A. | 2 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
分析 利用反比例函数图象上点的坐标性质得出ab=1,再利用分式的混合运算法则求出即可.
解答 解:∵点P(a,b)是反比例函数y=$\frac{1}{x}$图象上异于点(-1,-1)的一个动点,
∴ab=1,
∴$\frac{1}{1+a}$+$\frac{1}{1+b}$=$\frac{1+b}{(1+a)(1+b)}$+$\frac{1+a}{(1+a)(1+b)}$=$\frac{2+a+b}{1+a+b+ab}$=$\frac{2+a+b}{2+a+b}$=1.
故选:B.
点评 此题主要考查了反比例函数图象上点的坐标性质以及分式的混合运算,正确化简分式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列运算正确的是( )
| A. | x2•x3=x6 | B. | (x2)3=x6 | C. | x3+x2=x5 | D. | x+x2=x3 |
20.己知关于x的方程(a2-1)x2+(1-a)x+a-2=0,下列结论正确的是( )
| A. | 当a≠±1时,原方程是一元二次方程 | B. | 当a≠1时,原方程是一元二次方程 | ||
| C. | 当a≠-1时,原方程是一元二次方程 | D. | 原方程是一元二次方程 |
 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的2块带去,就能配一块大小和形状与原来都一样的三角形.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的2块带去,就能配一块大小和形状与原来都一样的三角形.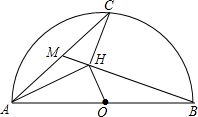 如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证:CH2=AH•OH.
如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证:CH2=AH•OH.