题目内容
某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
考点:分式方程的应用
专题:
分析:(1)设第一次购书的单价为x元,根据第一次用1200元购书若干本,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,列出方程,求出x的值即可得出答案;
(2)根据(1)先求出第一次和第二次购书数目,再根据卖书数目×(实际售价-当次进价)求出二次赚的钱数,再分别相加即可得出答案.
(2)根据(1)先求出第一次和第二次购书数目,再根据卖书数目×(实际售价-当次进价)求出二次赚的钱数,再分别相加即可得出答案.
解答:解:(1)设第一次购书的单价为x元,根据题意得:
+10=
.
解得:x=5.
经检验,x=5是原方程的解,
答:第一次购书的进价是5元;
(2)第一次购书为1200÷5=240(本),
第二次购书为240+10=250(本),
第一次赚钱为240×(7-5)=480(元),
第二次赚钱为200×(7-5×1.2)+50×(7×0.4-5×1.2)=40(元),
所以两次共赚钱480+40=520(元),
答:该老板两次售书总体上是赚钱了,共赚了520元.
| 1200 |
| x |
| 1500 |
| (1+20%)x |
解得:x=5.
经检验,x=5是原方程的解,
答:第一次购书的进价是5元;
(2)第一次购书为1200÷5=240(本),
第二次购书为240+10=250(本),
第一次赚钱为240×(7-5)=480(元),
第二次赚钱为200×(7-5×1.2)+50×(7×0.4-5×1.2)=40(元),
所以两次共赚钱480+40=520(元),
答:该老板两次售书总体上是赚钱了,共赚了520元.
点评:此题考查了分式方程的应用,掌握这次活动的流程,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对二次函数y=-x2-2x+2的图象描述正确的是( )
| A、与x轴有两个交点,对称轴在y轴的右侧 |
| B、与x轴有两个交点,对称轴在y轴的左侧 |
| C、与x轴没有交点,对称轴在y轴的左侧 |
| D、与x轴没有交点,对称轴在y轴的右侧 |
若⊙O半径为13,圆心在坐标原点上,点P的坐标为(5,12),则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、不能确定 |
 选项图中有四个正方体,只有一个是如图所示的纸片折叠而成的,请指出是哪一个?( )
选项图中有四个正方体,只有一个是如图所示的纸片折叠而成的,请指出是哪一个?( )



 如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为D,已知OD=5,则弦AC=
如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为D,已知OD=5,则弦AC= 如图,在平面直角坐标系xOy中,直线y1=k1x+b分别与x,y轴交于点B,A,与反比例函数y1=
如图,在平面直角坐标系xOy中,直线y1=k1x+b分别与x,y轴交于点B,A,与反比例函数y1=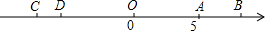 如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.
如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11. 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°.求证:AB∥CD.
如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°.求证:AB∥CD.