题目内容
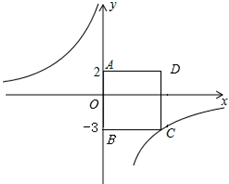 如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.
考点:待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征
专题:
分析:(1)先由点A的坐标为(0,2),点B的坐标为(0,-3)得到AB=5,则点C的坐标为(5,-3),根据反比例函数图象上点的坐标特征得k=-15,则反比例函数的解析式为y=-
;
(2)设点P到AD的距离为h,利用△PAD的面积恰好等于正方形ABCD的面积得到h=10,再分类讨论:当点P在第二象限时,则P点的纵坐标yP=h+2=12,可求的P点的横坐标,得到点P的坐标为(-
,12);②当点P在第四象限时,P点的纵坐标为yP=-(h-2)=-8,再计算出P点的横坐标.于是得到点P的坐标为(
,-8).
| 15 |
| x |
(2)设点P到AD的距离为h,利用△PAD的面积恰好等于正方形ABCD的面积得到h=10,再分类讨论:当点P在第二象限时,则P点的纵坐标yP=h+2=12,可求的P点的横坐标,得到点P的坐标为(-
| 5 |
| 4 |
| 15 |
| 8 |
解答:解:(1)∵点A的坐标为(0,2),点B的坐标为(0,-3),
∴AB=5,
∵四边形ABCD为正方形,
∴点C的坐标为(5,-3),
∴k=5×(-3)=-15,
∴反比例函数的解析式为y=-
;
(2)设点P到AD的距离为h.
∵△PAD的面积恰好等于正方形ABCD的面积,
∴
×5×h=52,
解得h=10,
①当点P在第二象限时,yP=h+2=12,
此时,xP=
=-
,
∴点P的坐标为(-
,12),
②当点P在第四象限时,yP=-(h-2)=-8,
此时,xP=
=
,
∴点P的坐标为(
,-8).
综上所述,点P的坐标为(-
,12)或(
,-8).
∴AB=5,
∵四边形ABCD为正方形,
∴点C的坐标为(5,-3),
∴k=5×(-3)=-15,
∴反比例函数的解析式为y=-
| 15 |
| x |
(2)设点P到AD的距离为h.
∵△PAD的面积恰好等于正方形ABCD的面积,
∴
| 1 |
| 2 |
解得h=10,
①当点P在第二象限时,yP=h+2=12,
此时,xP=
| -15 |
| 12 |
| 5 |
| 4 |
∴点P的坐标为(-
| 5 |
| 4 |
②当点P在第四象限时,yP=-(h-2)=-8,
此时,xP=
| -15 |
| -8 |
| 15 |
| 8 |
∴点P的坐标为(
| 15 |
| 8 |
综上所述,点P的坐标为(-
| 5 |
| 4 |
| 15 |
| 8 |
点评:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);(2)把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.

练习册系列答案
相关题目
 有两棵树,一棵高6米,另一棵高3米,两树相距4米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了
有两棵树,一棵高6米,另一棵高3米,两树相距4米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了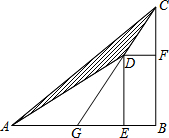 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?( )
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?( )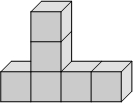 如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
 如图,点C在线段AB上,AD∥EB,AC=BE,∠ADC=∠BCE.
如图,点C在线段AB上,AD∥EB,AC=BE,∠ADC=∠BCE.