题目内容
8. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①a+b+c>0;②3a+b=0;③b2=4a(c-n); ④一元二次方程ax2+bx+c=n-1有两个不相等的实数根. 其中正确结论的个数是( )
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①a+b+c>0;②3a+b=0;③b2=4a(c-n); ④一元二次方程ax2+bx+c=n-1有两个不相等的实数根. 其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由定点坐标为(1,n),即可得出a+b+c>0,结论①正确;由抛物线的对称轴为直线x=1,可得出2a+b=0,结论②错误;由抛物线的对称轴及定点坐标,即可得出a+b+c=n、2a+b=0,进而即可得出b2=4ac-4an=4a(c-n),结论③正确;根据抛物线顶点的纵坐标为n,即可得出直线y=n-1与抛物线有两个交点,进而可得出一元二次方程ax2+bx+c=n-1有两个不相等的实数根,结论④正确.综上即可得出结论.
解答 解:当x=1时,
由图象可知:y=a+b+c>0,结论①正确;
抛物线对称轴为直线x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,结论②错误;
∵x=1时,y=n,
∴a+b+c=n.
∵2a+b=0,
∴a-2a+c=n,
∴c-a=n,
∴b2-4ac=4a2-4ac=4a(a-c)=-4an,
∴b2=4ac-4an=4a(c-n),结论③正确;
∵抛物线的顶点坐标为(1,n),
∴直线y=n与抛物线只有一个交点.
∵n-1<n,
∴直线y=n-1与抛物线有两个交点,
即一元二次方程ax2+bx+c=n-1有两个不相等的实数根,结论④正确.
综上所述:正确的结论有①③④.
故选C.
点评 本题考查二次函数的图象与系数的关系、抛物线与x轴的交点以及二次函数图象上点的坐标特征,根据函数图象逐一分析四条结论的正误是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.不等式组$\left\{\begin{array}{l}{2x+3<1}\\{2(x-2)>3x}\end{array}\right.$的解集是( )
| A. | x<-2 | B. | x<-4 | C. | -4<x<-2 | D. | 无解 |
1.在函数y=$\frac{2}{\sqrt{x-5}}$中,自变量x的取值范围是( )
| A. | x>5 | B. | x≥5 | C. | x≠5 | D. | x<5 |
16.已知△ABC的三边分别是6,8,10,则△ABC的面积是( )
| A. | 24 | B. | 30 | C. | 40 | D. | 48 |
13.下列由左边到右边的变形,是因式分解的是( )
| A. | am+bm-1=m(a+b)-1 | B. | (x+2)(x-5)=x2-3x-10 | C. | x2+5x+4=x(x+5+$\frac{4}{x}$) | D. | x2-4x=x(x-4) |
17.测得某人一根头发的直径约为0.000 071 5米,该数用科学记数法可表示为( )
| A. | 0.715×104 | B. | 0.715×10-4 | C. | 7.15×105 | D. | 7.15×10-5 |
18.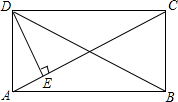 已知:如图,在矩形ABCD中,DE⊥AC于点E,∠ADE:∠CDE=1:2,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC于点E,∠ADE:∠CDE=1:2,那么∠BDC等于( )
 已知:如图,在矩形ABCD中,DE⊥AC于点E,∠ADE:∠CDE=1:2,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC于点E,∠ADE:∠CDE=1:2,那么∠BDC等于( )| A. | 60° | B. | 45° | C. | 22.5° | D. | 30° |