题目内容
16.已知△ABC的三边分别是6,8,10,则△ABC的面积是( )| A. | 24 | B. | 30 | C. | 40 | D. | 48 |
分析 因为△ABC的三边分别是6,8,10,根据勾股定理的逆定理可求出此三角形为直角三角形,根据三角形面积公式可求出面积.
解答 解:∵62+82=102,
∴△ABC是直角三角形,
∴△ABC的面积=$\frac{1}{2}$×6×8=24.
故选:A.
点评 本题考查勾股定理的逆定理,关键是根据三边长判断出为直角三角形,然后可求出三角形面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.在学习了命题后,七年级(3)班举行了一场知识竞赛,在“快问快答”环节,小舟选中的一道题目是这样的:“请举一个例子说明命题‘若|m|=|n|,则m=n’是假命题.”小舟的回答是“m=3,n=4”.你认为主持人接下来会对小舟说的是( )
| A. | “回答正确,加10分” | B. | “回答错误,例子可以是m=4,n=4” | ||
| C. | “回答错误,例子可以是m=-4,n=-4” | D. | “回答错误,例子可以是m=-4,n=4” |
1.已知x<y,则下列式子不正确的是( )
| A. | 4x<4y | B. | -4x<-4y | C. | x+4<y+4 | D. | x-4<y-4 |
5.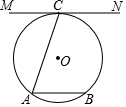 如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
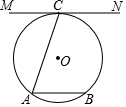 如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | 2 | D. | $\frac{\sqrt{5}}{2}$ |
6. 某篮球运动员在同一条件下进行“定点投篮”练习,结果如表所示:
某篮球运动员在同一条件下进行“定点投篮”练习,结果如表所示:
(1)补全上表;
(2)根据上表,画出该运动员投篮命中率变化的折线统计图;
(3)观察画出的折线统计图,投篮命中率的变化有什么规律?
 某篮球运动员在同一条件下进行“定点投篮”练习,结果如表所示:
某篮球运动员在同一条件下进行“定点投篮”练习,结果如表所示:| 投篮总次数n | 10 | 50 | 100 | 200 | 500 |
| 进球的次数m | 6 | 39 | 80 | 160 | 400 |
| 投篮命中率$\frac{m}{n}$ | 0.6 | 0.78 | 0.8 | 0.8 | 0.8 |
(2)根据上表,画出该运动员投篮命中率变化的折线统计图;
(3)观察画出的折线统计图,投篮命中率的变化有什么规律?
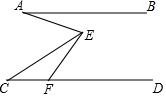 如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为36°或37°.
如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为36°或37°.
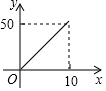
 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①a+b+c>0;②3a+b=0;③b2=4a(c-n); ④一元二次方程ax2+bx+c=n-1有两个不相等的实数根. 其中正确结论的个数是( )
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①a+b+c>0;②3a+b=0;③b2=4a(c-n); ④一元二次方程ax2+bx+c=n-1有两个不相等的实数根. 其中正确结论的个数是( )