题目内容
3.抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点的坐标为(-3,0),则与x轴另一个交点坐标为(5,0).分析 由抛物线的对称轴及抛物线与x轴的一个交点坐标,利用抛物线的对称性可求出另一交点坐标,此题得解.
解答 解:∵抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点的坐标为(-3,0),
∴抛物线与x轴的另一交点坐标为(5,0).
故答案为:(5,0).
点评 本题考查了抛物线与x轴的交点以及二次函数的性质,利用抛物线的对称性找出另一交点坐标是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
11.在学习了命题后,七年级(3)班举行了一场知识竞赛,在“快问快答”环节,小舟选中的一道题目是这样的:“请举一个例子说明命题‘若|m|=|n|,则m=n’是假命题.”小舟的回答是“m=3,n=4”.你认为主持人接下来会对小舟说的是( )
| A. | “回答正确,加10分” | B. | “回答错误,例子可以是m=4,n=4” | ||
| C. | “回答错误,例子可以是m=-4,n=-4” | D. | “回答错误,例子可以是m=-4,n=4” |
13.一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)在上述变化过程中,自变量是汽车行驶路程;因变量是邮箱内剩油量.
(2)用表格表示汽车从出发地行驶10千米、20千米、30千米、40千米时的剩油量.
请将表格补充完整:
(3)试写出y与x的关系式式y=56-0.08x.
(4)这辆汽车行驶350千米时剩油多少升?汽车剩油8升时,行驶了多少千米?
(1)在上述变化过程中,自变量是汽车行驶路程;因变量是邮箱内剩油量.
(2)用表格表示汽车从出发地行驶10千米、20千米、30千米、40千米时的剩油量.
请将表格补充完整:
| 行驶路程x(千米) | 100 | 200 | 300 | 400 |
| 油箱内剩油量y(升) | 40 | 24 |
(4)这辆汽车行驶350千米时剩油多少升?汽车剩油8升时,行驶了多少千米?
 如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠A0B内部建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且点P到两条公路l1、l2的距离也相等.请用尺规作图作出点P.(不写作法,保留作图痕迹)
如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠A0B内部建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且点P到两条公路l1、l2的距离也相等.请用尺规作图作出点P.(不写作法,保留作图痕迹)
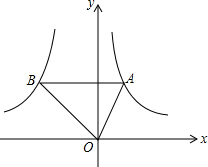 如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.
如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①a+b+c>0;②3a+b=0;③b2=4a(c-n); ④一元二次方程ax2+bx+c=n-1有两个不相等的实数根. 其中正确结论的个数是( )
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(0,3)和(0,4)之间.则下列结论:①a+b+c>0;②3a+b=0;③b2=4a(c-n); ④一元二次方程ax2+bx+c=n-1有两个不相等的实数根. 其中正确结论的个数是( )