题目内容
1．已知a+b=8，a-b=4，则a2-b2=32．分析 先根据平方差公式变形，再代入求出即可．
解答 解：∵a+b=8，a-b=4，
∴a2-b2=（a+b）（a-b）=8×4=32，
故答案为：32．
点评 本题考查了平方差公式，能熟记平方差公式是解此题的关键．
练习册系列答案
相关题目
9．
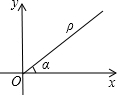如图，在平面直角坐标系中，设点P到原点O的距离为ρ，OP与x轴正方向的交角为a，则用[ρ，a]表示点P的极坐标，例如：点P的坐标为（1，1），则其极坐标为[$\sqrt{2}$，45°]．若点Q的极坐标为[4，120°]，则点Q的平面坐标为（ ）
如图，在平面直角坐标系中，设点P到原点O的距离为ρ，OP与x轴正方向的交角为a，则用[ρ，a]表示点P的极坐标，例如：点P的坐标为（1，1），则其极坐标为[$\sqrt{2}$，45°]．若点Q的极坐标为[4，120°]，则点Q的平面坐标为（ ）| A． | （-2，2$\sqrt{3}$） | B． | （2，-2$\sqrt{3}$） | C． | （-2$\sqrt{3}$，-2） | D． | （-4，-4$\sqrt{3}$） |
如图，直线AB、CD相交于点O，OM⊥AB于点O，若∠MOD=43°，则∠COB=133度．
6．
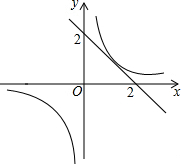如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点，则b的取值范围是（ ）
如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点，则b的取值范围是（ ）| A． | b＞2 | B． | -2＜b＜2 | C． | b＞2或b＜-2 | D． | b＜-2 |
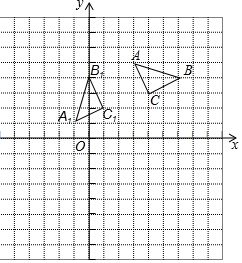如图，平面直角坐标系建立在边长为1个单位长度的小正方形组成的网格中，格点△ABC的顶点在网格线的交点上，将△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1．