题目内容
13.已知点P(3,-4)绕O逆时针旋转90°得到对应点P′的坐标为(4,3).分析 设P′(m,n),(m、n>0),由OA⊥OB且|OA|=|OB|,可得-$\frac{4}{3}$•$\frac{n}{m}$=-1,$\sqrt{{3}^{2}+{4}^{2}}$=$\sqrt{{m}^{2}+{n}^{2}}$,解之可得m、n的值.
解答 解:设P′(m,n),(m、n>0),
由OA⊥OB,且|OA|=|OB|,
可得-$\frac{4}{3}$•$\frac{n}{m}$=-1,$\sqrt{{3}^{2}+{4}^{2}}$=$\sqrt{{m}^{2}+{n}^{2}}$,
解得:m=4,n=3,
∴点P′的坐标为(4,3),
故答案为:(4,3).
点评 本题主要考查坐标与图形的变化-旋转,熟练掌握旋转的性质及两点间的距离公式和直线垂直的性质是解题的关键.

练习册系列答案
相关题目
3.圆柱共有( )个面.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.对于反比例函数y=-$\frac{3}{x}$,下列说法不正确的是( )
| A. | 图象经过点(1,-3) | |
| B. | 图象分布在第二、四象限 | |
| C. | 当x>0时,y随x的增大而增大 | |
| D. | 点A(x1,y1)、B(x2、y2)都在反比例函数y=-$\frac{3}{x}$的图象上,若x1<x2,则y1<y2 |
5. 如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )
如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )
 如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )
如图,已知平面直角坐标系中有点A(1,1),B(1,5),C(3,1),且双曲线y=$\frac{k}{x}$与△ABC有公共点,则k的取值范围是( )| A. | 1≤k≤3 | B. | 3≤k≤5 | C. | 1≤k≤5 | D. | 1≤k≤$\frac{49}{8}$ |
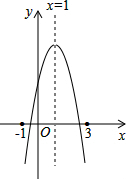 如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )
如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( ) 如图,一个用篱笆围成的长方形的面积是500m2.
如图,一个用篱笆围成的长方形的面积是500m2.