题目内容
已知实数a,b,c满足a+b+c=1,
+
+
=1,求abc的值.
| 1 |
| a+b-c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
考点:分式的化简求值
专题:
分析:首先求出a+b-c=1-2c,b+c-a=1-2a,c+a-b=1-2b,得到
+
+
=
,借助
+
+
=1,即可解决问题.
| 1 |
| a+b-c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
| 3-4(a+b+c)+4(ab+ac+bc) |
| 1-2(a+b+c)+4(ab+ac+bc)-8abc |
| 1 |
| a+b-c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
解答:解:∵a+b+c=1,
∴a+b-c=1-2c,b+c-a=1-2a,c+a-b=1-2b,
∴
+
+
=
+
+
=
=
=
,
∵
+
+
=1,
∴-1+4(ab+ac+bc)=-1+4(ab+ac+bc)-8abc,
∴abc=0.
∴a+b-c=1-2c,b+c-a=1-2a,c+a-b=1-2b,
∴
| 1 |
| a+b-c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
=
| 1 |
| 1-2a |
| 1 |
| 1-2b |
| 1 |
| 1-2c |
=
| (1-2b)(1-2c)+(1-2a)(1-2c)+(1-2a)(1-2b) |
| (1-2a)(1-2b)(1-2c) |
=
| 1-2c-2b+4bc+1-2c-2a+4ac+1-2b-2a+4ab |
| (1-2a-2b+4ab)(1-2c) |
=
| 3-4(a+b+c)+4(ab+ac+bc) |
| 1-2(a+b+c)+4(ab+ac+bc)-8abc |
∵
| 1 |
| a+b-c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
∴-1+4(ab+ac+bc)=-1+4(ab+ac+bc)-8abc,
∴abc=0.
点评:该题主要考查了分式的混合运算法则及其应用问题;灵活运用分式的混合运算法则来变形、化简、运算是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若27a3nb3m与-5b6a3是同类项,则m+n=( )
| A、2 | B、3 | C、4 | D、5 |
等腰三角形的一个角是80°,则它的顶角的度数是( )
| A、30° |
| B、80°或20° |
| C、80°或50° |
| D、20° |
一个扇形的圆心角为120°,半径为15cm,则它的弧长为( )
| A、5πcm | B、10πcm |
| C、15πcm | D、20πcm |
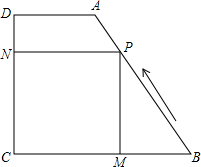 如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB=
如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB=
 已知关于x的方程x2-kx+k-1=0.
已知关于x的方程x2-kx+k-1=0.