题目内容
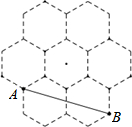 蜂槽的构造非常美丽、科学,如图是由7个形状、大小完全相同的边长为1cm的正六边形组成,则线段AB的长为
蜂槽的构造非常美丽、科学,如图是由7个形状、大小完全相同的边长为1cm的正六边形组成,则线段AB的长为考点:正多边形和圆
专题:
分析:过点D作DE⊥AC于点E,先根据正六边形的性质求出其内角的度数,再根据等腰三角形的性质求出∠DAE的度数,由直角三角形的性质得出AE的长,进而可得出AF的长,同理可得出AF=CF,再根据勾股定理求出AB的长即可.
解答: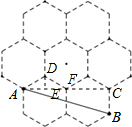 解:过点D作DE⊥AC于点E,
解:过点D作DE⊥AC于点E,
∵图中各多边形是正六边形,
∴其内角的度数=
=120°.
∵AD=DF,
∴∠DAE=
=30°.
∵正六边形的边长为1cm,
∴AE=AD•cos30°=1×
=
,
∴AF=2AE=
.
同理,CF=AF=
,
∴AC=2
.
∵∠FCE=30°,
∴∠ACB=120°-90°=30°,
∴AB=
=
=
(cm).
故答案为:
cm.
 解:过点D作DE⊥AC于点E,
解:过点D作DE⊥AC于点E,∵图中各多边形是正六边形,
∴其内角的度数=
| (6-2)×180° |
| 6 |
∵AD=DF,
∴∠DAE=
| 180°-120° |
| 2 |
∵正六边形的边长为1cm,
∴AE=AD•cos30°=1×
| ||
| 2 |
| ||
| 2 |
∴AF=2AE=
| 3 |
同理,CF=AF=
| 3 |
∴AC=2
| 3 |
∵∠FCE=30°,
∴∠ACB=120°-90°=30°,
∴AB=
| AC2+BC2 |
(2
|
| 13 |
故答案为:
| 13 |
点评:本题考查的是正多边形和圆,熟知正六边形的性质是解答此题的关键.

练习册系列答案
相关题目
等腰三角形的一个角是80°,则它的顶角的度数是( )
| A、30° |
| B、80°或20° |
| C、80°或50° |
| D、20° |
如果3m表示向北走3m,那么-2m与6m分别表示( )
| A、向北走2m,向南走6m |
| B、向北走2m,向北走6m |
| C、向南走2m,向南走6m |
| D、向南走2m,向北走6m |
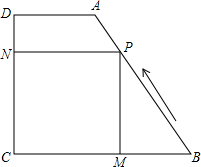 如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB=
如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB= 如图,梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一动点,那么PC+PD的最小值为
如图,梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一动点,那么PC+PD的最小值为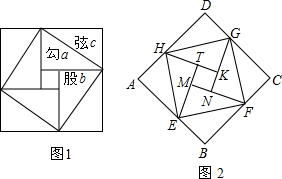
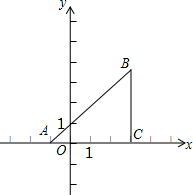 如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.
如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.