题目内容
已知二次方程x2+ax+b=0有两个连续的整数根,二次方程x2+bx+a=0有整数根,求a,b的值.
考点:一元二次方程的整数根与有理根
专题:
分析:可设x2+ax+b=0的两根为n,n+1(n是整数),则2n+1=-a,n(n+1)=b,则方程x2+bx+a=0可以改写为x2+n(n+1)x-(2n+1)=0①,分两种情况:(1)若n≥0,则方程①有一正一负两根;(2)若n≤-1,则方程①有两个负整数根;进行讨论即可得到a,b的值.
解答:解:设x2+ax+b=0的两根为n,n+1(n是整数),则2n+1=-a,n(n+1)=b,
则方程x2+bx+a=0可以改写为x2+n(n+1)x-(2n+1)=0①,
(1)若n≥0,则方程①有一正一负两根,
设其正整数根为m,则
m2+n(n+1)m-(2n+1)=0②,
即mn2+(m-2)n+(m2-1)=0,
∵n是整数,
∴△=(m-2)2-4m(m2-1)≥0,
整理为4m≤
+1,
若m≥2,则上式不成立,故0<m<2,
则m=1,
将m=1代入方程②得n2-n=0,
解得n=0,1.
当n=0时,a=-1,b=0;
当n=1时,a=-3,b=2;
(2)若n≤-1,则方程①有两个负整数根,
即△=n2(n+1)2+4(2n+1)应为完全平方数,且为偶数,
由于n≤-1,则n2(n+1)2+4(2n+1)<[n(n+1)]2,
故n2(n+1)2+4(2n+1)≤[n(n+1)-2]2,
因此n2+3n≤0,即n=-3,-2,-1,
经检验,n=-2,-1时,方程①无实根,
当n=-3时,方程①为x2+6x+5=0,
其两根为-1,-5,此时a=5,b=6,
综合(1)(2)可知,a,b的值为-1,0或-3,2或5,6.
则方程x2+bx+a=0可以改写为x2+n(n+1)x-(2n+1)=0①,
(1)若n≥0,则方程①有一正一负两根,
设其正整数根为m,则
m2+n(n+1)m-(2n+1)=0②,
即mn2+(m-2)n+(m2-1)=0,
∵n是整数,
∴△=(m-2)2-4m(m2-1)≥0,
整理为4m≤
| 4 |
| m2 |
若m≥2,则上式不成立,故0<m<2,
则m=1,
将m=1代入方程②得n2-n=0,
解得n=0,1.
当n=0时,a=-1,b=0;
当n=1时,a=-3,b=2;
(2)若n≤-1,则方程①有两个负整数根,
即△=n2(n+1)2+4(2n+1)应为完全平方数,且为偶数,
由于n≤-1,则n2(n+1)2+4(2n+1)<[n(n+1)]2,
故n2(n+1)2+4(2n+1)≤[n(n+1)-2]2,
因此n2+3n≤0,即n=-3,-2,-1,
经检验,n=-2,-1时,方程①无实根,
当n=-3时,方程①为x2+6x+5=0,
其两根为-1,-5,此时a=5,b=6,
综合(1)(2)可知,a,b的值为-1,0或-3,2或5,6.
点评:考查了一元二次方程的整数根和有理根,关键是设x2+ax+b=0的两根为n,n+1(n是整数),则2n+1=-a,n(n+1)=b,将方程x2+bx+a=0改写为x2+n(n+1)x-(2n+1)=0①,以及分类思想的应用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
下列各组代数式能合并同类项的是( )
| A、3与x | ||
| B、3xy与-2yx2 | ||
| C、2a2b3与-4a3b2c | ||
D、m和
|
我国教育事业快速发展,今年普通高校招生人数达698万人,用科学记数法表示698万人为( )
| A、6.98×102人 |
| B、69.8×105人 |
| C、6.98×106人 |
| D、0.698×107人 |
等腰三角形的一个角是80°,则它的顶角的度数是( )
| A、30° |
| B、80°或20° |
| C、80°或50° |
| D、20° |
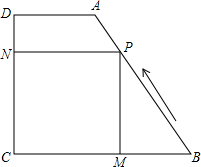 如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB=
如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB= 如图,梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一动点,那么PC+PD的最小值为
如图,梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一动点,那么PC+PD的最小值为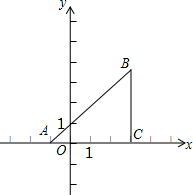 如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.
如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.