题目内容
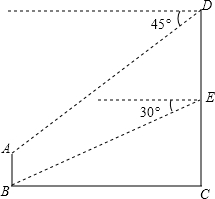 在小明和小刚家的楼前有一盏路灯AB,高为4m,小明家在3楼的E处,他站在窗口看B处的俯角为30°.小刚家在D处,他站在窗口看A处的俯角为45°,路灯与楼的距离为20m.你能知道小刚家大约是几楼吗?
在小明和小刚家的楼前有一盏路灯AB,高为4m,小明家在3楼的E处,他站在窗口看B处的俯角为30°.小刚家在D处,他站在窗口看A处的俯角为45°,路灯与楼的距离为20m.你能知道小刚家大约是几楼吗?考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点A作AF垂直CD于点F,根据在E处看B处的俯角为30°,在D处看A处的俯角为45°,BC=20m,分别求出EC和DF的长度,然后根据小明家在3楼,求出每层楼的高度,然后即可求出小刚家的楼层.
解答:解: 过点A作AF垂直CD于点F,
过点A作AF垂直CD于点F,
则有四边形ABCF为矩形,
AB=CF,BC=AF,
在Rt△BCF中,
∵∠EBC=30°,BC=20m,
∴EC=BC•tan30°=
(m),
在Rt△ADF中,
∵∠ADF=45°,
∴DF=AF=20(m),
∵AB=4m,
∴DC=DF+FC=24(m),
∵小明家在三楼,
∴每层楼的高度为:EC÷2=
(m),
24÷
≈4.
则小刚家的楼层为5楼.
答:小刚家大约是5楼.
 过点A作AF垂直CD于点F,
过点A作AF垂直CD于点F,则有四边形ABCF为矩形,
AB=CF,BC=AF,
在Rt△BCF中,
∵∠EBC=30°,BC=20m,
∴EC=BC•tan30°=
| 20 |
| 3 |
| 3 |
在Rt△ADF中,
∵∠ADF=45°,
∴DF=AF=20(m),
∵AB=4m,
∴DC=DF+FC=24(m),
∵小明家在三楼,
∴每层楼的高度为:EC÷2=
| 10 |
| 3 |
| 3 |
24÷
| 10 |
| 3 |
| 3 |
则小刚家的楼层为5楼.
答:小刚家大约是5楼.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用公共边求解直角三角形,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
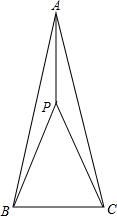 在△ABC中,AB=AC,∠BAC=30°,点P为△ABC内一点,PA=2,PB=
在△ABC中,AB=AC,∠BAC=30°,点P为△ABC内一点,PA=2,PB=