题目内容
15.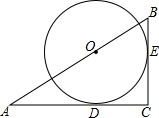 如图,△ABC中,∠C=90°,以AB上一点O为圆心的⊙O分别与AC、BC相切于D,E,若AC=4,BC=3,求⊙O的半径.
如图,△ABC中,∠C=90°,以AB上一点O为圆心的⊙O分别与AC、BC相切于D,E,若AC=4,BC=3,求⊙O的半径.
分析 连接OD,OE,根据S△AOC+S△BOC=S△ABC,即$\frac{1}{2}$AC•OD+$\frac{1}{2}$BC•OE=$\frac{1}{2}$AC•BC即可求解.
解答 解:连接OD,OE,设OD=r,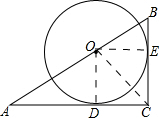
∵AC,BC切⊙O于D,E
∴∠ODC=∠OEC=∠DCE=90°,CD=CE,
∴OD=OE
∵S△AOC+S△BOC=S△ABC
$\frac{1}{2}$AC•OD+$\frac{1}{2}$BC•OE=$\frac{1}{2}$AC•BC
即$\frac{1}{2}$×4r+$\frac{1}{2}$×3r=$\frac{1}{2}$×4×3,
解得r=$\frac{12}{7}$.
答:⊙O的半径为$\frac{12}{7}$.
点评 本题考查的是切线性质的实际应用,关键是运用切线的性质可证明四边形ODCE正方形,根据三角形的面积的公式就可以求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.图中,∠1与∠2是同位角的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列判断错误的是( )
| A. | 若x=y,则xm-5=ym-5 | B. | 若(a2+1)x=1,则x=$\frac{1}{{a}^{2}+1}$ | ||
| C. | 若x2=3x,则x=3 | D. | 若m=n,则am=an |
20. 如图,∠1=45°,∠3=105°,则∠2的度数为( )
如图,∠1=45°,∠3=105°,则∠2的度数为( )
 如图,∠1=45°,∠3=105°,则∠2的度数为( )
如图,∠1=45°,∠3=105°,则∠2的度数为( )| A. | 60° | B. | 55° | C. | 35° | D. | 30° |

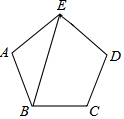 如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.
如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.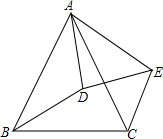 如图:已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE,求证:AB=AC.
如图:已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE,求证:AB=AC.