题目内容
18.如果$\frac{a}{b}$=$\frac{2}{3}$,那么$\frac{b-a}{a+b}$=$\frac{1}{5}$.分析 利用比例的性质由$\frac{a}{b}$=$\frac{2}{3}$得到$\frac{a}{2}$=$\frac{b}{3}$,则可设a=2t,b=3t,然后把a=2t,b=3t代入$\frac{b-a}{a+b}$中进行分式的运算即可.
解答 解:∵$\frac{a}{b}$=$\frac{2}{3}$,
∴$\frac{a}{2}$=$\frac{b}{3}$,
设a=2t,b=3t,
∴$\frac{b-a}{a+b}$=$\frac{3t-2t}{2t+3t}$=$\frac{1}{5}$.
故答案为$\frac{1}{5}$.
点评 本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列命题中,逆命题是真命题的是( )
| A. | 直角三角形的两锐角互余 | B. | 对顶角相等 | ||
| C. | 若两直线垂直,则两直线有交点 | D. | 若x=1,则x2=1 |
6.为了考察甲、乙两种小麦,分别从中抽取5株苗测得苗高(单位:cm)
甲:2,4,6,8,10;
乙:1,3,5,7,9.
用S甲2和S乙2分别表示两个样本的方差,则( )
甲:2,4,6,8,10;
乙:1,3,5,7,9.
用S甲2和S乙2分别表示两个样本的方差,则( )
| A. | S甲2>S乙2 | B. | S甲2<S乙2 | C. | S甲2=S乙2 | D. | 无法确定 |
8.如果点A(2,m)在抛物线y=x2上,将抛物线向右平移3个单位后,点A同时平移到点A′,那么A′坐标为( )
| A. | (2,1) | B. | (2,7) | C. | (5,4) | D. | (-1,4) |
 如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.
如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.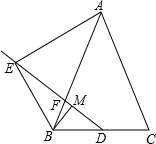 如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.
如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.