题目内容
1.下列一元二次方程中,总有两个不相等实数根的是( )| A. | 2x2+4x+2=0 | B. | x2+4x+5=0 | C. | x2+2014x-2015=0 | D. | 3x2+1=0 |
分析 判断上述方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了.
解答 解:A、△=b2-4ac=42-4×2×2=0,方程有两个相等的实数根;
B、△=b2-4ac=42-4×1×5=-4<0,方程没有实数根;
C、△=b2-4ac=20142-4×1×2015>0,方程有两个不相等的实数根;
D、△=b2-4ac=02-4×3×1=-12<0,方程没有实数根.
故选:C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,弦AC∥OB,∠B=25°,则∠O=( )
如图,弦AC∥OB,∠B=25°,则∠O=( )
 如图,弦AC∥OB,∠B=25°,则∠O=( )
如图,弦AC∥OB,∠B=25°,则∠O=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
6.方程(x+2)2-10(x+2)+25=0的解为( )
| A. | -2 | B. | 2 | C. | -3 | D. | x1=x2=3 |
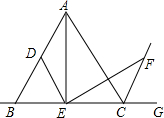 如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.
如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF. (1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;
(1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;