题目内容
12．一小艇在江面上顺流航行63千米到目的地，然后逆流回航到出发地，航行时间共5小时20分．已知水流速度为每小时3千米，小艇在静水中的速度是多少？小艇顺流航行时间和逆流回航时间各是多少？分析 设小艇在静水中的速度是x千米/小时，则顺流速度为x+3千米/小时，逆流速度为x-3千米/小时，根据顺流航行63千米到目的地，然后逆流回航到出发地，航行时间共5小时20分列方程解答；进一步求得顺流航行时间和逆流回航时间即可．
解答 解：设小艇在静水中的速度是x千米/小时，由题意得
$\frac{63}{x+3}$+$\frac{63}{x-3}$=5$\frac{20}{60}$
整理得8x2-189x-72=0，
解得：x1=24，x2=-$\frac{3}{8}$（舍去），
经检验x=24是原分式方程的解，
则顺水航行时间$\frac{63}{x+3}$=$\frac{7}{3}$小时，
逆水航行时间$\frac{63}{x-3}$=3小时，
答：小艇在静水中的速度是24千米/小时，则顺流航行时间为$\frac{7}{3}$小时，逆流航行时为3小时．
点评 此题考查分式方程的实际运用，掌握顺流速度、逆流速度、静水速度、水流速度之间的关系是解决问题的关键．
练习册系列答案
相关题目
2．某车间的生产任务是平均每天生产某种零件200个；由于各种原因，实际每天生产量与计划量相比有出入，下表是某一周的生产情况纪录（超产为正，不足为负）．
（1）根据记录情况，前两天共生产零件403个；
（2）产量最多的一天比产量最少的一天多生产26个；
（3）为调动工人生产积极性，该车间实行计件工资制，即每生产l个零件记60元，超额完成任务的每个另外奖15元，少生产一个扣15元，则该车间工人这一周的工资总额是多少元？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -8 |
（2）产量最多的一天比产量最少的一天多生产26个；
（3）为调动工人生产积极性，该车间实行计件工资制，即每生产l个零件记60元，超额完成任务的每个另外奖15元，少生产一个扣15元，则该车间工人这一周的工资总额是多少元？
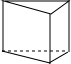如图所示的是一个棱柱，请问：
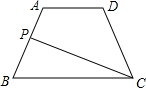如图，在等腰梯形ABCD中，已知AD∥BC，AB=10，BC=15，tanB=$\frac{4}{3}$，点P是AB边上的一个动点．设BP=x，△BPC的面积为y，求y关于x的函数关系式，并写出x的取值范围．
4．若数轴上的点M对应的数是-2$\frac{2}{3}$，那么与M相距1个单位长度的点N对应的数是（ ）
| A． | -1$\frac{1}{3}$ | B． | -3$\frac{2}{3}$ | C． | -3$\frac{2}{3}$与-1$\frac{2}{3}$ | D． | -3$\frac{2}{3}$与-1$\frac{1}{3}$ |