题目内容
在Rt△ABC中,∠ACB=90°,∠A=30°,AC=
cm,则AB边上的中线长为( )
| 3 |
| A、1cm | ||
| B、1.5cm | ||
| C、2cm | ||
D、
|
考点:直角三角形斜边上的中线
专题:
分析:设斜边AB=2x,根据直角三角形30°角所对的直角边等于斜边的一半可得BC=x,再利用勾股定理列式求出x的值,从而得到AB,然后根据直角三角形斜边上的中线等于斜边的一半解答.
解答: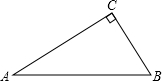 解:设斜边AB=2x,
解:设斜边AB=2x,
∵∠ACB=90°,∠A=30°,
∴BC=
AB=x,
由勾股定理得,AB2=AC2+BC2,
即(2x)2=(
)2+x2,
解得x=1,
∴AB=2×1=2cm,
AB边上的中线长=
AB=
×2=1cm.
故选A.
 解:设斜边AB=2x,
解:设斜边AB=2x,∵∠ACB=90°,∠A=30°,
∴BC=
| 1 |
| 2 |
由勾股定理得,AB2=AC2+BC2,
即(2x)2=(
| 3 |
解得x=1,
∴AB=2×1=2cm,
AB边上的中线长=
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,直角三角形30°角所对的直角边等于斜边的一半的性质以及勾股定理,熟记性质并列出方程是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
已知a,b,c是实数,且a>b>c,则下列选项正确的是( )
| A、a+b>b+c | ||||
| B、a-b>b-c | ||||
| C、ab>bc | ||||
D、
|
下列运算正确的是( )
| A、-(a-1)=-a-1 |
| B、(2a3)2=4a6 |
| C、(a-b)2=a2-b2 |
| D、a3+a2=2a5 |
下列计算正确的是( )
| A、(a5)2=a7 |
| B、b3•b3=2b3 |
| C、a3÷a=a3 |
| D、a3•a2=a5 |
已知某条经过原点的直线还经过点(2,1),下列结论正确的是( )
| A、直线的解析式为y=2x |
| B、函数图象经过二、四象限 |
| C、函数图象一定经过点(-2,-1) |
| D、y随x的增大而减小 |
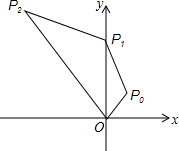 如图,在直角坐标系中,点P0的坐标为(
如图,在直角坐标系中,点P0的坐标为(



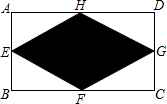 已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为( )
已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为( )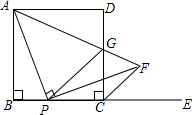 如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.