题目内容
某商场用2500元购进A、B两种新型节能灯共50盏,这两种灯的进价、售价如下表所示.
(1)这两种灯各购进多少盏?全部销售完总利润是多少?
(2)该商场购进的50盏节能灯很快售完,计划再购进五十盏A、B种型号的新型节能灯,在进价和售价都不变的情况下,计划销售完这批台灯的总利润不少于1400元,问至少购进B①形台灯多少盏?
| 类型 价格 |
A型 | B型 |
| 进价 (元/盏) |
40 | 65 |
| 售价(元/盏) | 60 | 100 |
(2)该商场购进的50盏节能灯很快售完,计划再购进五十盏A、B种型号的新型节能灯,在进价和售价都不变的情况下,计划销售完这批台灯的总利润不少于1400元,问至少购进B①形台灯多少盏?
考点:二元一次方程组的应用,一元一次不等式的应用
专题:
分析:(1)设购进A、B两种灯分别为x、y盏,根据总共50盏灯,花费2500元,可得出方程组,解出即可;
(2)设购进B型灯m盏,根据这批台灯的总利润不少于1400元,可得出不等式,解出即可得出答案.
(2)设购进B型灯m盏,根据这批台灯的总利润不少于1400元,可得出不等式,解出即可得出答案.
解答:解:(1)设购进A、B两种灯分别为x、y盏,
由题意得,
,
解得:
.
总利润=(60-40)×30+(100-65)×20=1300元.
(2)设购进B型灯m盏,
则(60-40)(50-m)+(100-65)m≥1400,
解得:m≥26
.
答:至少要购进B型灯27盏.
由题意得,
|
解得:
|
总利润=(60-40)×30+(100-65)×20=1300元.
(2)设购进B型灯m盏,
则(60-40)(50-m)+(100-65)m≥1400,
解得:m≥26
| 2 |
| 3 |
答:至少要购进B型灯27盏.
点评:本题考查了二元一次方程组及一元一次不等式的知识,解答本题的关键是仔细审题,将实际问题转化为数学思想求解.

练习册系列答案
相关题目
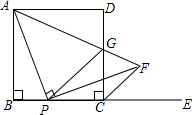 如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG. 如图,∠1=∠2,∠3=100°,求∠4的度数.
如图,∠1=∠2,∠3=100°,求∠4的度数.