Question

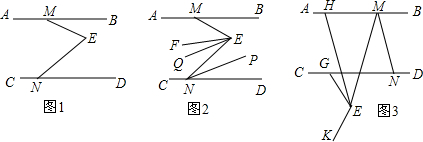
13．已知：直线AB∥CD，点M，N分别在直线AB，CD上，点E为平面内一点．
（1）如图1，∠BME，∠E，∠END的数量关系为∠E=∠BME+∠END；（直接写出答案）
（2）如图2，∠BME=m°，EF平分∠MEN，NP平分∠END，EQ∥NP，求∠FEQ的度数．（用含m的式子表示）
（3）如图3点G为CD上一点，∠BMN=n•∠EMN，∠GEK=n•∠GEM，EH∥MN交AB于点H，探究∠GEK，∠BMN，∠GEH之间的数量关系（用含n的式子表示）

Answer 1

分析 （1）过点E作l∥AB，利用平行线的性质可得∠1=∠BME，∠2=∠DNE，由∠MEN=∠1+∠2，等量代换可得结论；
（2）利用角平分线的性质可得$∠NEF=\frac{1}{2}∠MEN，∠ENP=\frac{1}{2}∠END$，由EQ∥NP，可得$∠QEN=∠ENP=\frac{1}{2}∠END$，由（1）的结论可得∠MEN=∠BME+∠END，等量代换得出结论；
（3）由已知可得$∠EMN=\frac{1}{n}∠BMN$，$∠GEM=\frac{1}{n}∠GEK$，由EH∥MN，可得$∠HEM=∠ENM=\frac{1}{n}∠BMN$，因为∠GEH=∠GEM-∠HEM，等量代换得出结论．

解答 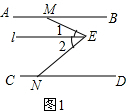解：（1）如图1，过点E作l∥AB，
∵AB∥CD，
∴l∥AB∥CD，
∴∠1=∠BME，∠2=∠DNE，
∵∠MEN=∠1+∠2，
∴∠E=∠BME+∠END，
故答案为：∠E=∠BME+∠END；

（2）如图2，∵EF平分∠MEN，NP平分∠END，
∴$∠NEF=\frac{1}{2}∠MEN，∠ENP=\frac{1}{2}∠END$，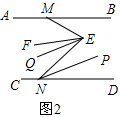
∵EQ∥NP，
∴$∠QEN=∠ENP=\frac{1}{2}∠END$，
∵∠MEN=∠BME+∠END，
∴∠MEN-∠END=∠BME=m°，
∴∠FEQ=∠NEF-∠NEQ
=$\frac{1}{2}∠MEN-\frac{1}{2}∠END$，
=$\frac{1}{2}（∠MEN-∠END）$
=$\frac{1}{2}$m°；

（3）n∠GEH=∠GEK-∠BMN．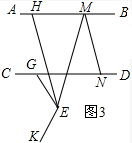
如图3，∵∠BMN=n•∠EMN，∠GEK=n•∠GEM，
∴$∠EMN=\frac{1}{n}∠BMN$，$∠GEM=\frac{1}{n}∠GEK$，
∵EH∥MN，
∴$∠HEM=∠ENM=\frac{1}{n}∠BMN$，
∵∠GEH=∠GEM-∠HEM，
=$\frac{1}{n}∠GEK-\frac{1}{n}∠BMN$，
∴n∠GEH=∠GEK-∠BMN．

点评 本题主要考查了平行线的性质，作出适当的辅助线，结合图形等量代换是解答此题的关键．