题目内容
2.不等式组:$\left\{\begin{array}{l}{x+6≤3x+4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$的解集为1≤x<4.分析 先求出不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x+6≤3x+4①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$
∵解不等式①得:x≥1,
解不等式②得:x<4,
∴不等式组的解集为1≤x<4.
故答案为:1≤x<4.
点评 本题考查了解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
相关题目
14.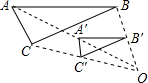 如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
 如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不确定 |
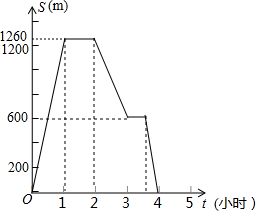 张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题:
张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题: