题目内容
6.我们把一直角边是另一直角边2倍的直角三角形称为“倍勾三角形”,如图1,在△ABC中,AB=3,AC=2$\sqrt{2}$,∠BAC=45°,CD⊥AB于D.P是射线AB上的一个动点(不与D重合),E是线段PC的中点,将点E绕点P顺时针方向旋转90°得到点F,连接FB,FC,FP.(1)下列三角形:①△PCF,②△DCB,③△DCA,其中是“倍勾三角形”的有①②(填序号);
(2)求证:CB⊥BF;
(3)连接FA,如图2,当F,E,A三点在一直线上时,△BCF是否为“倍勾三角形”,如果是,请证明;如果不是,求$\frac{BF}{BC}$的值;
(4)当△BCF为“倍勾三角形”时,直接写出所有可能的AP的长度.
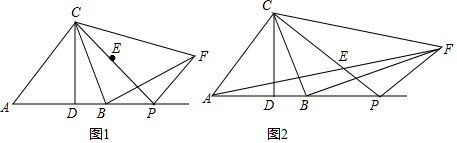
分析 (1)求出AD、CD、DB的长即可判断;
(2)由△CDB∽△CPF,推出∠CBD=∠MBP=∠CFB,由△MBP∽△MFC,推出$\frac{MB}{MF}$=$\frac{MP}{MC}$,推出$\frac{MB}{MP}$=$\frac{MF}{MC}$,又∠M=∠M,即可推出△MCP∽△MFB,推出∠MCP=∠MFB,又∠COB=∠FOP,即可推出∠CBO=∠OPF=90°;
(3)由题意:PE=PF=CE,∠PEF=∠AEC=45°,设PF=PE=CE=a,由∠AEC=∠EAP+∠APE,∠CAD=∠CAD+∠EAP=45°,推出∠CAE=∠CPA,由∠ACE=∠ACP,推出△ACE∽△PCA,推出AC2=CE•CP,推出2a2=(2$\sqrt{2}$)2,推出a=2,推出PC=4,CD=2,PC=2CD,推出∠CPD=30°,∠DCP=∠BCF=60°,推出∠CFB=30°,推出BF=$\sqrt{3}$BC,推出△BCF不是“倍勾三角形”;
(4)三种情形条件即可①如图3中,当BC=2BF时,作FH⊥AB于H.②如图4中,同法可以假设FH=x,BH=2x,想办法构建方程即可解决问题.
解答 解:(1)如图1中,
∵CD⊥AB,∠A=45°,AB=2$\sqrt{2}$,
∴AD=CD=2,∵AB=3,
∴BD=AB-AD=1,
∴CD=2BD,
∴△CDB是“倍勾三角形”,
∵∠CPF=90°,PC=2PF,
∴△PCF是“倍勾三角形”,
故答案为①②.
(2)如图1-1中,设BF交PC于O,延长CB交FP的延长线于M.
∵△CDB,△CPF都是“倍勾三角形”,
∴△CDB∽△CPF,
∴∠CBD=∠MBP=∠CFB,∵∠BMP=∠CMF,
∴△MBP∽△MFC,
∴$\frac{MB}{MF}$=$\frac{MP}{MC}$,
∴$\frac{MB}{MP}$=$\frac{MF}{MC}$,∵∠M=∠M,
∴△MCP∽△MFB,
∴∠MCP=∠MFB,∵∠COB=∠FOP,
∴∠CBO=∠OPF=90°,
∴CB⊥BF.
(3)结论:△BCF不是“倍勾三角形”,
理由:如图2中,
由题意:PE=PF=CE,∠PEF=∠AEC=45°,
设PF=PE=CE=a,
∵∠AEC=∠EAP+∠APE,∠CAD=∠CAD+∠EAP=45°,
∴∠CAE=∠CPA,∵∠ACE=∠ACP,
∴△ACE∽△PCA,
∴AC2=CE•CP,
∴2a2=(2$\sqrt{2}$)2,
∴a=2,
∴PC=4,CD=2,PC=2CD,
∴∠CPD=30°,∠DCP=∠BCF=60°,
∴∠CFB=30°,
∴BF=$\sqrt{3}$BC,
∴△BCF不是“倍勾三角形”,
∴$\frac{BF}{BC}$=$\sqrt{3}$.
(4)如图3中,当BC=2BF时,作FH⊥AB于H.
易证∠DCB=∠FBH,
∴tan∠DCB=tan∠FBH=$\frac{1}{2}$=$\frac{FH}{BH}$,设FH=x,BH=2x,
在Rt△BFH中,x2+(2x)2=($\frac{\sqrt{5}}{2}$)2,
解得x=$\frac{1}{2}$,
∴BH=1,
∴C、D、H、F共线,
易证△PDC∽△FDP,可得PD2=CD•DF=1,
∴PD=1,AP=AD-PD=1.
如图4中,同法可以假设FH=x,BH=2x,
在Rt△BFH中,x2+(2x)2=($\frac{1}{2}$$\sqrt{5}$)2,或x2+(2x)2=(2$\sqrt{5}$)2,
解得x=$\frac{1}{2}$或2,
设PB=y,由△CDP∽△PHF,
∴$\frac{CD}{PH}$=$\frac{DP}{FH}$,
∴$\frac{2}{1-y}$=$\frac{1+y}{\frac{1}{2}}$或$\frac{2}{4-y}$=$\frac{1+y}{2}$,
解得y=0或3,
∴AP=3或6,
综上所述,满足条件的AP的值为1或3或6.
点评 本题考查相似三角形综合题、等腰直角三角形的性质、勾股定理、“倍勾三角形”的定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. | k≤-4 | B. | k≥-4 | C. | k≤4 | D. | k>4 |

| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
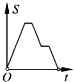
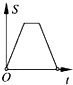
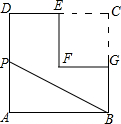 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )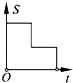
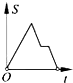
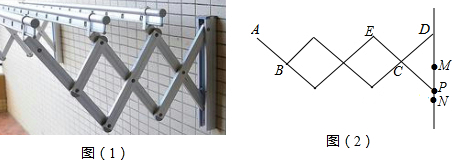
 如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)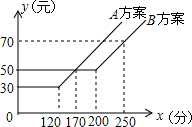 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论: