题目内容
某商场将多于2000千克的苹果分为两种不同等级进行销售,一等果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=3x2+100;二等果从开始销售至销售的第x天的总销量y2(千克)与x的关系为y2=2x2+40x;销售完毕时发现,两种等级水果销售完的天数相同,并且一等果的总销量比二等果的少200千克.
(1)求苹果的总质量;
(2)如果一等果的利润为每千克4元,二等果的利润是每千克1元,求从第几天开始一等果销售利润大于二等果日销售利润?
(1)求苹果的总质量;
(2)如果一等果的利润为每千克4元,二等果的利润是每千克1元,求从第几天开始一等果销售利润大于二等果日销售利润?
考点:二次函数的应用
专题:
分析:(1)由题意y2-y1=200建立方程求出x的值就可以求出两种等级的苹果的质量,从而求出总质量;
(2)设第x天的销量为M,先求出第x天的销量,设总利润为W,由总利润=每千克利润×数量表示两种等级的苹果的利润W与x之间的关系式,再建立不等式组求出其解即可.
(2)设第x天的销量为M,先求出第x天的销量,设总利润为W,由总利润=每千克利润×数量表示两种等级的苹果的利润W与x之间的关系式,再建立不等式组求出其解即可.
解答:解:(1)由题意,得
2x2+40x-(3x2+100)=200
解得:x1=10,x2=30.
∵苹果的总质量为:2x2+40x+3x2+100=5x2+40x+100.
当x=10时,苹果的总质量为5×100+40×10+100=1000千克<2000千克,舍去.
当x=30时,苹果的总质量为5×900+40×30+100=5800千克>2000千克,
∴苹果的总质量为:5800.
(2)设第x天的销量为M,
∴M1=3x2+100-3(x-1)2+100=6x-3,
M2=2x2+40x-2(x-1)2-40(x-1)=4x+38
设第x天一等果的利润为W1元,二等果的利润为W2元,由题意,得
W1=24x-12,W2=4x+38.
∵一等果销售利润大于二等果日销售利润,
∴24x-12>4x+38,
∴x>
,
∴第3天开始一等果销售利润大于二等果日销售利润.
2x2+40x-(3x2+100)=200
解得:x1=10,x2=30.
∵苹果的总质量为:2x2+40x+3x2+100=5x2+40x+100.
当x=10时,苹果的总质量为5×100+40×10+100=1000千克<2000千克,舍去.
当x=30时,苹果的总质量为5×900+40×30+100=5800千克>2000千克,
∴苹果的总质量为:5800.
(2)设第x天的销量为M,
∴M1=3x2+100-3(x-1)2+100=6x-3,
M2=2x2+40x-2(x-1)2-40(x-1)=4x+38
设第x天一等果的利润为W1元,二等果的利润为W2元,由题意,得
W1=24x-12,W2=4x+38.
∵一等果销售利润大于二等果日销售利润,
∴24x-12>4x+38,
∴x>
| 5 |
| 2 |
∴第3天开始一等果销售利润大于二等果日销售利润.
点评:本题考查了一元二次方程的解法的运用,二次函数的解析式的运用,销售问题的总利润=每件利润×数量的运用,解答时求出利润与时间x的关系式是关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 如图,AB∥CD,DB⊥BC,∠1=39°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=39°,则∠2的度数是( )| A、151° | B、141° |
| C、61° | D、51° |
若关于x的不等式
的整数解共有5个,则m的取值范围是( )
|
| A、7≤m≤8 |
| B、7≤m<8 |
| C、7<m≤8 |
| D、7<m<8 |
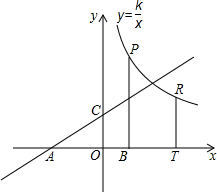 如图,直线y=
如图,直线y=
 如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于
如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于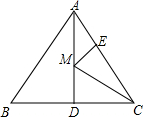 如图,等边△ABC的边长为6,面积为9
如图,等边△ABC的边长为6,面积为9