题目内容
 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:二次函数图象与系数的关系,抛物线与x轴的交点
专题:
分析:①根据抛物线的对称轴为直线x=-
=2,则有4a+b=0;
②观察函数图象得到当x=-3时,函数值小于0,则9a-3b+c<0,即9a+c<3b;
③由于x=-1时,y=0,则a-b+c=0,易得c=-5a,所以8a+7b+2c=8a-28a-10a=-30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;
④由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小;
⑤由抛物线的对称轴为直线x=2,与x轴的一个交点为(-1,0),得出抛物线与x轴的另外一个交点为(5,0),再根据抛物线开口向下得出当函数值y<0时,自变量x的取值范围是x<-1或x>5.
| b |
| 2a |
②观察函数图象得到当x=-3时,函数值小于0,则9a-3b+c<0,即9a+c<3b;
③由于x=-1时,y=0,则a-b+c=0,易得c=-5a,所以8a+7b+2c=8a-28a-10a=-30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;
④由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小;
⑤由抛物线的对称轴为直线x=2,与x轴的一个交点为(-1,0),得出抛物线与x轴的另外一个交点为(5,0),再根据抛物线开口向下得出当函数值y<0时,自变量x的取值范围是x<-1或x>5.
解答:解:①∵抛物线的对称轴为直线x=-
=2,
∴b=-4a,即4a+b=0,故本结论正确;
②∵当x=-3时,y<0,
∴9a-3b+c<0,
即9a+c<3b,故本结论错误;
③∵抛物线与x轴的一个交点为(-1,0),
∴a-b+c=0,
而b=-4a,
∴a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,故本结论正确;
④∵对称轴为直线x=2,
∴当-1<x<2时,y的值随x值的增大而增大,
当x>2时,y随x的增大而减小,故本结论错误;
⑤∵抛物线的对称轴为直线x=2,与x轴的一个交点为(-1,0),
∴抛物线与x轴的另外一个交点为(5,0),
∴当函数值y<0时,自变量x的取值范围是x<-1或x>5,故本结论正确.
故选:B.
| b |
| 2a |
∴b=-4a,即4a+b=0,故本结论正确;
②∵当x=-3时,y<0,
∴9a-3b+c<0,
即9a+c<3b,故本结论错误;
③∵抛物线与x轴的一个交点为(-1,0),
∴a-b+c=0,
而b=-4a,
∴a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,故本结论正确;
④∵对称轴为直线x=2,
∴当-1<x<2时,y的值随x值的增大而增大,
当x>2时,y随x的增大而减小,故本结论错误;
⑤∵抛物线的对称轴为直线x=2,与x轴的一个交点为(-1,0),
∴抛物线与x轴的另外一个交点为(5,0),
∴当函数值y<0时,自变量x的取值范围是x<-1或x>5,故本结论正确.
故选:B.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
二次函数y=x2-2x-3上有两点:(-1,y1),(4,y2),下列结论正确的是( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法确定 |
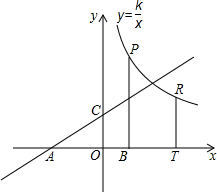 如图,直线y=
如图,直线y= 如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于
如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于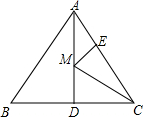 如图,等边△ABC的边长为6,面积为9
如图,等边△ABC的边长为6,面积为9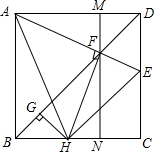 已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
 a、b在数轴上的位置如图所示,那么化简|b-a|的结果是
a、b在数轴上的位置如图所示,那么化简|b-a|的结果是