题目内容
19.对于实数p,我们规定:用<p>表示不小于p的最小整数,例如:<4>=4,<$\sqrt{3}$>=2.现对72进行如下操作:72$\stackrel{第一次}{→}$<$\sqrt{72}$>=9$\stackrel{第二次}{→}$<$\sqrt{9}$>=3$\stackrel{第三次}{→}$<$\sqrt{3}$>=2.即对72只需进行3次操作后变为2,类似地:
(1)对36只需进行3次操作后变为2;
(2)只需进行3次操作后变为2的所有正整数中,最大的是256.
分析 (1)根据题目中的例子可以解答本题;
(2)根据题意可以求得只需进行3次操作后变为2的所有正整数中,最大的是哪个整数.
解答 解:(1)由题意可得,
36$\stackrel{第一次}{→}$<$\sqrt{36}$>=6$\stackrel{第二次}{→}$<$\sqrt{6}$>=3$\stackrel{第三次}{→}$<$\sqrt{3}$>=2,
故答案为:3;
(2)由题意可得,
256$\stackrel{第一次}{→}$<$\sqrt{256}$>=16$\stackrel{第二次}{→}$<$\sqrt{16}$>=4$\stackrel{第三次}{→}$<$\sqrt{4}$>=2,
故只需进行3次操作后变为2的所有正整数中,最大的是256,
故答案为:256.
点评 本题考查估计无理数的大小、实数大小的比较,解答本题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
7.在△ABC中,∠B=30°,点D在BC边上,点E在AC边上,AD=BD,DE=CE,若△ADE为等腰三角形,则∠C的度数为( )
| A. | 20° | B. | 20°或30° | C. | 30°或40° | D. | 20°或40° |
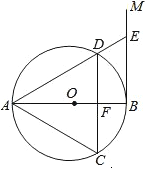 如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.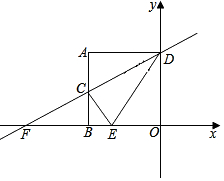 如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且AD∥OB,AB∥OD,点C为AB的中点,直线CD交x轴于点F.
如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且AD∥OB,AB∥OD,点C为AB的中点,直线CD交x轴于点F.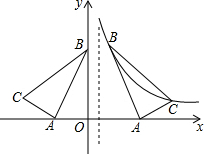 如图,在平面直角坐标系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),点C在第二象限且tan∠ACB=2,将Rt△ABC沿平行于y轴的某条直线翻折,得Rt△A1B1C1,若点B1,C1恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则k的值等于$\frac{16}{3}$.
如图,在平面直角坐标系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),点C在第二象限且tan∠ACB=2,将Rt△ABC沿平行于y轴的某条直线翻折,得Rt△A1B1C1,若点B1,C1恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则k的值等于$\frac{16}{3}$.