题目内容
6.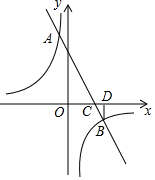 如图,已知一次函数y1=k1x+6与反比例函数y2=$\frac{{k}_{2}}{x}$相交于A、B,与x轴交于点C,过点B作BD⊥x轴于点D,已知sin∠DBC=$\frac{\sqrt{5}}{5}$,OC:CD=3:1.
如图,已知一次函数y1=k1x+6与反比例函数y2=$\frac{{k}_{2}}{x}$相交于A、B,与x轴交于点C,过点B作BD⊥x轴于点D,已知sin∠DBC=$\frac{\sqrt{5}}{5}$,OC:CD=3:1.(1)求y1和y2的解析式;
(2)连接OA,OB,求△AOB的面积.
分析 (1)根据平行线的性质得到$\frac{BD}{OE}$=$\frac{CD}{OC}$=$\frac{1}{3}$,求出BD,根据正弦的概念求出CD、BC,利用待定系数法求出函数解析式;
(2)求出A、B的纵坐标,根据三角形的面积公式计算即可.
解答 解:(1)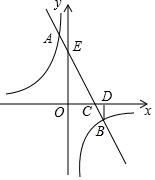 y1=k1x+6与y轴的交点E的坐标为(0,6),
y1=k1x+6与y轴的交点E的坐标为(0,6),
∴OE=6,
∵BD⊥x轴,
∴OE∥BD,
∴$\frac{BD}{OE}$=$\frac{CD}{OC}$=$\frac{1}{3}$,
∴BD=2,
∵sin∠DBC=$\frac{\sqrt{5}}{5}$,
∴设CD=$\sqrt{5}$x,则BC=5x,
由勾股定理得,(5x)2=($\sqrt{5}$x)2+4,
解得,x=$\frac{\sqrt{5}}{5}$,
则CD=$\sqrt{5}$x=1,则BC=5x=$\sqrt{5}$,
∴点B的坐标为(4,-2),
-2=k1×4+6,
解得,k1=-2,
则y1=-2x+6,y2=-$\frac{8}{x}$;
(2)$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=-2x+6}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=8}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=-2}\end{array}\right.$,
则△AOB的面积=$\frac{1}{2}$×3×8+$\frac{1}{2}×$3×2=15.
点评 本题考查的是反比例函数与一次函数的交点问题、解直角三角形的应用,掌握待定系数法求函数解析式的一般步骤、方程组的解法是解题的关键.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案| A. | 10 | B. | 5$\sqrt{2}$ | C. | 5$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
①任意两个等边三角形相似
②顶角对应相等的两个等腰三角形相似
③两条边对应成比例的两个直角三角形相似
其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
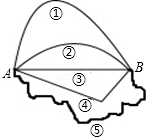 如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.
如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.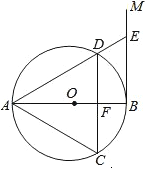 如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.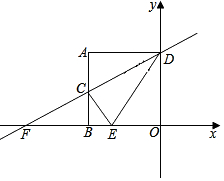 如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且AD∥OB,AB∥OD,点C为AB的中点,直线CD交x轴于点F.
如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且AD∥OB,AB∥OD,点C为AB的中点,直线CD交x轴于点F.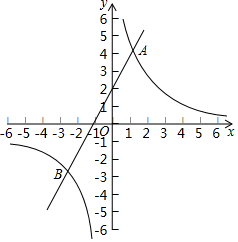 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).