题目内容
 如图,矩形ABCD的外接圆O与水平地面相切于点A,圆O的半径为4,且
如图,矩形ABCD的外接圆O与水平地面相切于点A,圆O的半径为4,且 |
| BC |
 |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:切线的性质,弧长的计算,旋转的性质
专题:应用题
分析:根据题意得出圆的周长以及圆转动的周数,进而得出与地面相切的弧.
解答:解:∵圆O半径为4,
∴圆的周长为:2π×r=8π,
∵将圆O向右滚动,使得O点向右移动了98π,
∴98π÷8π=12…3π,
即圆滚动12周后,又向右滚动了3π,
∵矩形ABCD的外接圆O与水平地面相切于A点,
=2
,
∴
=
×8π=
π<3π,
+
=
×8π=4π>3π,
∴此时
与地面相切;
故选:B.
∴圆的周长为:2π×r=8π,
∵将圆O向右滚动,使得O点向右移动了98π,
∴98π÷8π=12…3π,
即圆滚动12周后,又向右滚动了3π,
∵矩形ABCD的外接圆O与水平地面相切于A点,
 |
| BC |
 |
| AB |
∴
 |
| AB |
| 1 |
| 6 |
| 4 |
| 3 |
 |
| AB |
 |
| BC |
| 1 |
| 2 |
∴此时
 |
| BC |
故选:B.
点评:此题主要考查了旋转的性质以及圆的周长公式等知识,得出O点转动的周数是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
在平面直角坐标系中,点A坐标为(1,3),将点A向左平移2个单位长度,得到点A′,则点A′的坐标为( )
| A、(3,3) |
| B、(-1,3) |
| C、(0,3) |
| D、(3,-1) |
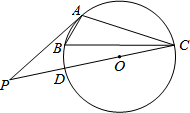 如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.



 如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是
如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是