题目内容
 如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是
如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是考点:余角和补角,角平分线的定义
专题:
分析:先根据角平分线的性质求出∠COD的度数,由两角互余的性质求出∠AOC的度数,根据∠AOB=∠AOC+∠BOC即可得出结论.
解答: 解:∵OD平分∠BOC,∠BOC=50°,
解:∵OD平分∠BOC,∠BOC=50°,
∴∠COD=
∠BOC=
×50°=25°.
∵AOC和∠COD互余,
∴∠AOC=90°-25°=65°,
∴∠AOB=∠AOC+∠BOC=65°+50°=115°.
故答案为:115°.
 解:∵OD平分∠BOC,∠BOC=50°,
解:∵OD平分∠BOC,∠BOC=50°,∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AOC和∠COD互余,
∴∠AOC=90°-25°=65°,
∴∠AOB=∠AOC+∠BOC=65°+50°=115°.
故答案为:115°.
点评:本题考查的是余角和补角,熟知两角互余的定义是解答此题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图,矩形ABCD的外接圆O与水平地面相切于点A,圆O的半径为4,且
如图,矩形ABCD的外接圆O与水平地面相切于点A,圆O的半径为4,且 |
| BC |
 |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cosB的值等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若a<b,则下列各式中一定成立的是( )
| A、a-1<b-1 |
| B、2a>2b |
| C、-a<-b |
| D、ac<bc |
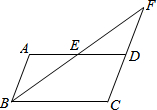 如图,在?ABCD中,AB=AE,连接BE且延长CD的延长线于点F.求证:AD=CF.
如图,在?ABCD中,AB=AE,连接BE且延长CD的延长线于点F.求证:AD=CF. 如图,在△ABC和△ADE中,B,D,E,C在同一条直线上,下面给出三个条件:
如图,在△ABC和△ADE中,B,D,E,C在同一条直线上,下面给出三个条件: