题目内容
16. 如图,在菱形ABCD中,对角线AC、BD相交于点O,点E、F分别是边AB、BC的中点,连接EF,若EF=3,BD=6$\sqrt{3}$,则菱形ABCD的面积为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,点E、F分别是边AB、BC的中点,连接EF,若EF=3,BD=6$\sqrt{3}$,则菱形ABCD的面积为( )| A. | 6$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 18$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
分析 根据EF是△ABC的中位线,根据三角形中位线定理求的AC的长,然后根据菱形的面积公式求解.
解答 解:∵E、F是AB和BC的中点,即EF是△ABC的中位线,
∴AC=2EF=6,
则S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×6$\sqrt{3}$=18$\sqrt{3}$,
故选C.
点评 本题考查了三角形的中位线定理和菱形的面积公式,理解中位线定理求的AC的长是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
4.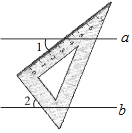 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )| A. | 37° | B. | 53° | C. | 63° | D. | 27° |
11.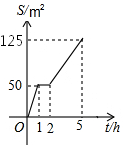 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )| A. | 75m2 | B. | 50m2 | C. | 31.25m2 | D. | 25m2 |
5.下列4个图案中,是轴对称图形的个数为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.
如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由. 如图,已知点A(-1,0)、B(4,0)是抛物线y=ax2+bx-4与x轴的两个交点,点C是抛物线与y轴的交点,连接AC,抛物线的对称轴与x轴交于点M.
如图,已知点A(-1,0)、B(4,0)是抛物线y=ax2+bx-4与x轴的两个交点,点C是抛物线与y轴的交点,连接AC,抛物线的对称轴与x轴交于点M.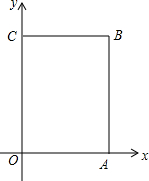 已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)
已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)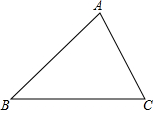 如图,已知△ABC中,AB=4,AC=3.
如图,已知△ABC中,AB=4,AC=3.