题目内容
11．
如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD=30°，则∠BAD为（ ）| A． | 30° | B． | 50° | C． | 60° | D． | 70° |
分析 连接BD，根据直径所对的圆周角是直角，得∠ADB=90°，根据同弧或等弧所对的圆周角相等，得∠ABD=∠ACD，从而可得到∠BAD的度数．
解答 
解：连接BD，
∵∠ACD=30°，
∴∠ABD=30°，
∵AB为直径，
∴∠ADB=90°，
∴∠BAD=90°-∠ABD=60°．
故选C．
点评 本题考查了圆周角定理，解答本题的关键是掌握圆周角定理中在同圆或等圆中，同弧或等弧所对的圆周角相等．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
1．
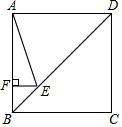如果，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则BE的长为（ ）
如果，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则BE的长为（ ）| A． | 1 | B． | $\sqrt{2}$-1 | C． | 2$\sqrt{2}$-2 | D． | 4$\sqrt{2}$-4 |
2．下列四个数中，最小的是（ ）
| A． | -3 | B． | -2 | C． | 3 | D． | 5 |
6．
一个几何体是由一些大小相同的小立方块摆成的，其主视图和俯视图如图所示，则组成这个几何体的小立方块最少有（ ）
一个几何体是由一些大小相同的小立方块摆成的，其主视图和俯视图如图所示，则组成这个几何体的小立方块最少有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
16．下列计算正确的是（ ）
| A． | a6÷a3=a2 | B． | （ab3）3=ab6 | C． | （a+2）2=a2+4 | D． | x12÷x6=x6 |
20．计算：（2x2）3-6x3（x3+2x2+x）=（ ）
| A． | -12x5-6x4 | B． | 2x6+12x5+6x4 | C． | x2-6x-3 | D． | 2x6-12x5-6x4 |
如图，已知点A（-1，0）、B（4，0）是抛物线y=ax2+bx-4与x轴的两个交点，点C是抛物线与y轴的交点，连接AC，抛物线的对称轴与x轴交于点M．