题目内容
17.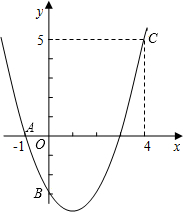 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.(1)观察图象写出A、B、C三点的坐标,并求出此二次函数的解析式;
(2)求出此抛物线的顶点坐标和对称轴.
分析 (1)根据二次函数的图象直接写出A、B、C三点的坐标,进一步利用待定系数法求得函数解析式即可;
(2)化为顶点式求得此抛物线的顶点坐标和对称轴.
解答 解:(1)根据二次函数的图象可知:
A(-1,0),B(0,-3),C(4,5),
把A(-1,0),B(0,-3),C(4,5)代入y=ax2+bx+c可得
$\left\{\begin{array}{l}{a-b+c=0}\\{c=-3}\\{16a+4b+c=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$.
即二次函数的解析式为y=x2-2x-3;
(2)∵y=x2-2x-3=y=(x-1)2-4,
∴此抛物线的顶点坐标(1,-4),和对称轴x=1.
点评 此题考查二次函数的性质,待定系数法求函数解析式,关键是掌握待定系数法的方法与步骤,正确得出各个点的坐标.

练习册系列答案
相关题目
7.青山村种的水稻2010年平均每公顷产7200kg,2012年水稻平均每公顷产的产量是8400kg,设水稻每公顷产量的年平均增长率为x,可列方程为( )
| A. | 7200(1+x)2=8400 | B. | 7200(1+x2)=8400 | C. | 7200(x2+x)=8400 | D. | 7200(1+x)=8400 |
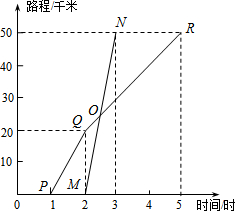 已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题: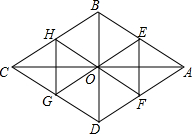 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.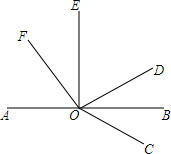 如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.
如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.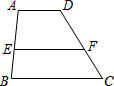 四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.
四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.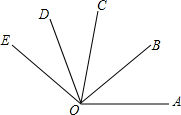 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,求∠BOD的度数.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,求∠BOD的度数.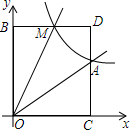 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).