题目内容
12．
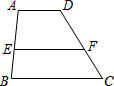四边形ABCD中，E、F分别为AB、CD上的点，且AD∥EF∥BC，AE：EB=3：2，AD=2cm，BC=4cm，则EF=$\frac{16}{5}$cm．
分析 连接AC交EF于G，根据平行线分线段成比例定理分别求出EG、GF的长即可．
解答 解：
连接AC交EF于G，
∵EF∥BC，AE：EB=3：2，
∴$\frac{EG}{BC}$=$\frac{AE}{AB}$=$\frac{3}{5}$，又BC=4cm，
∴EG=$\frac{12}{5}$，
同理FG=$\frac{4}{5}$，
∴EF=EG+GF=$\frac{16}{5}$cm，
故答案为：$\frac{16}{5}$．
点评 本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
10．
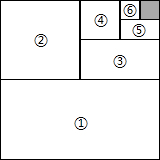如图，将一个边长为1的正方形纸片分割成7个部分，部分①是边长为1的正方形纸片面积的一半，部分 ②是部分①面积的一半，部分 ③是部分②面积的一半，依此类推，$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{2015}}$的值为（ ）
如图，将一个边长为1的正方形纸片分割成7个部分，部分①是边长为1的正方形纸片面积的一半，部分 ②是部分①面积的一半，部分 ③是部分②面积的一半，依此类推，$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{2015}}$的值为（ ）| A． | $\frac{1}{{2}^{2015}}$ | B． | 1-$\frac{1}{{2}^{2015}}$ | C． | $\frac{1}{{2}^{4030}}$ | D． | 不能确定 |
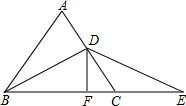已知，如图，△ABC是等边三角形，BD是AC边上的高，延长BC到E，使CE=CD，过D作DF⊥BE于F．
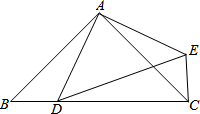如图，△ABC是等腰直角三角形，AB=$4\sqrt{2}$，D为斜边BC上的一点（D与B、C均不重合），连结AD，把△ABD绕点A按逆时针旋转后得到△ACE，连结DE，设BD=x．
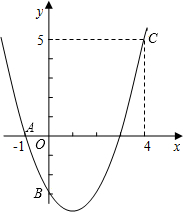如图，二次函数y=ax2+bx+c的图象经过A、B、C三点．
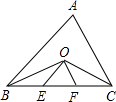如图，在△ABC中，∠ABC和∠ACB的平分线交于点O，过点O分别作OE∥AB，OF∥AC，交BC于点E、F，∠BOC=130°，则∠EOF=80．