题目内容
2.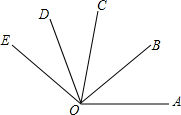 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,求∠BOD的度数.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,求∠BOD的度数.解:∵OB是∠AOC的角平分线
∴∠AOB=∠BOC=40°
∵OD是∠COE的角平分线
∴∠COE=∠DOE=$\frac{1}{2}$∠COE,
∵∠COE=60°
∴∠COD=30°,
∴∠BOD=∠COD+∠BOC=30°+40°=70°.
分析 根据OB是∠AOC的角平分线,∠AOB=40°,可以求出∠BOC=40°,OD是∠COE的角平分线,∠COE=60°,得出∠COD=30°,两角相加得∠BOD.
解答 解:∵OB是∠AOC的角平分线
∴∠AOB=∠BOC=40°
∵OD是∠COE的角平分线
∴∠COD=∠DOE=$\frac{1}{2}$∠COE,
∵∠COE=60°
∴∠COD=30°,
∴∠BOD=∠COD+∠BOC=30°+40°=70°.
故答案为:∠BOC,∠DOE,∠COE,∠COD=30°,∠BOC,30°,40°,70°.
点评 题目考察角平分线的定义,根据角平分线定义,得角平分线可以平分角的度数.题目整体较为简单.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
11.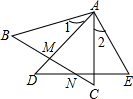 如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
 如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
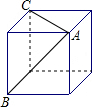 如图,在一个正方体的2个面上画了两条对角线AB、AC,那么这两条对角线的夹角是60°.
如图,在一个正方体的2个面上画了两条对角线AB、AC,那么这两条对角线的夹角是60°. 如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,求BC2的值.
如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,求BC2的值.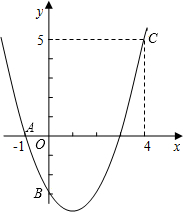 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.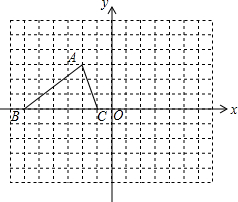 如图,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
如图,把△ABC置于平面直角坐标系中,请你按下列要求分别画图: