题目内容
15.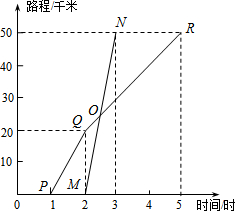 已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:(1)直接写出:甲出发1小时后,乙才开始出发;乙的速度为50千米/时;甲骑自行车在全程的平均速度为12.5千米/时.
(2)求乙出发几小时后就追上了甲?
(3)求乙出发几小时后与甲相距10千米?
分析 (1)根据函数图象可以解答本题;
(2)根据函数图象分别设出QR段和MN段对应的函数解析式,求出这两个函数的解析式,然后联立方程组即可求得乙出发几小时后追上甲;
(3)根据第二问求得的两个函数的解析式和函数图象,可知两个函数作差的绝对值等于10或10t=40,从而可以求得乙出发几小时与甲相距10千米.
解答 解:(1)根据函数图象可得,
甲出发1小时后,乙才开始出发;乙的速度为:50÷(3-2)=50千米/时;甲骑自行车在全程的平均速度是:50÷(5-1)=12.5千米/时;
故答案为:1,50,12.5;
(2)设QR段对应的函数解析式为:s=kt+b,
∵点(2,20),(5,50)在QR段上,
∴$\left\{\begin{array}{l}{2k+b=20}\\{5k+b=50}\end{array}\right.$,
解得k=10,b=0.
即QR段对应的函数解析式为:s=10t;
设过点M(2,0),N(3,50)的函数解析式为:s=mt+n,
则$\left\{\begin{array}{l}{2m+n=0}\\{3m+n=50}\end{array}\right.$,
解得m=50,n=-100.
即过点M(2,0),N(3,50)的函数解析式为:s=50t-100;
∴$\left\{\begin{array}{l}{s=10t}\\{s=50t-100}\end{array}\right.$
解得,t=2.5,s=25
2.5-2=0.5(小时),
即乙出发0.5小时后就追上甲;
(3)根据题意可得,
|50t-100-10t|=10或10t=40,
解得t1=2.25,t2=2.75,t3=4,
∴2.25-2=0.25(小时),2.75-2=0.75(小时),4-2=2(小时),
即乙出发0.25小时或0.75小时或2小时时与甲相距10千米.
点评 本题考查一次函数的应用,解题的关键是利用数形结合的思想找出所求问题需要的条件.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | 正方形 | B. | 矩形 | ||
| C. | 菱形 | D. | 邻边相等的四边形 |
| A. | (a-b)2=a2-b2 | B. | (-a-b)2=a2+2ab-b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a-b)2=a2-2ab-b2 |
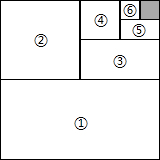 如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分 ②是部分①面积的一半,部分 ③是部分②面积的一半,依此类推,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{2015}}$的值为( )
如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分 ②是部分①面积的一半,部分 ③是部分②面积的一半,依此类推,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{2015}}$的值为( )| A. | $\frac{1}{{2}^{2015}}$ | B. | 1-$\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{4030}}$ | D. | 不能确定 |
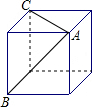 如图,在一个正方体的2个面上画了两条对角线AB、AC,那么这两条对角线的夹角是60°.
如图,在一个正方体的2个面上画了两条对角线AB、AC,那么这两条对角线的夹角是60°.



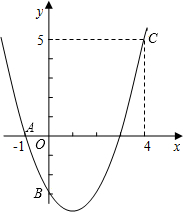 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.