Question

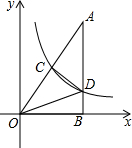如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=

k

x

（x＞0）经过斜边OA的中点C，与另一直角边交于点D．若S_△OCD=12，则S_△OBD的值为

 

．

Answer 1

考点：反比例函数系数k的几何意义

专题：

分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=

1

2

|k|．

解答：解：如图，过C点作CE⊥x轴，垂足为E．
∵Rt△OAB中，∠OBA=90°，
∴CE∥AB，
∵C为Rt△OAB斜边OA的中点C，
∴CE为Rt△OAB的中位线，
∵△OEC∽△OBA，
∴

OC

OA

=

1

2

．
∵双曲线的解析式是y=

k

x

（x＞0），即xy=k
∴S_△OBD=S_△COE=

1

2

|k|，
∴S_△AOB=4S_△COE=2|k|，
由S_△AOB-S_△OBD=S_△AOD=2S_△DOC=24，得2k-

1

2

k=24，
k=16，
S_△OBD=S_△COE=

1

2

k=8．
故答案为：8．

点评：本题考查了反比函数k的几何意义，过图象上的任意一点作x轴、y轴的垂线，所得三角形的面积是

1

2

|k|，是经常考查的知识点，也体现了数形结合的思想．