题目内容
某种植物的主干长出若干数目的支干,每个支干又长出同一数量的小分支,主干、支干和小分支的总数是57,设每个支干长出x个小分支,则可列方程正确的是( )
| A、x2+x(x+1)+x+1=57 |
| B、(x+1)2=57 |
| C、x2+x+1=57 |
| D、x(x+1)=57 |
考点:由实际问题抽象出一元二次方程
专题:
分析:由题意设每个支干长出的小分支的数目是x个,每个小分支又长出x个分支,则又长出x2个分支,则共有x2+x+1个分支,即可列方程.
解答:解:设每个支干长出的小分支的数目是x个,
根据题意列方程得:x2+x+1=57.
故选C.
根据题意列方程得:x2+x+1=57.
故选C.
点评:此题考查了一元二次方程的应用,要根据题意分别表示主干、支干、小分支的数目,列方程求解,注意能够熟练运用因式分解法解方程.

练习册系列答案
相关题目
小明上学骑自行车的速度是其步行速度的2.5倍,若小明的步行速度为a m/s,则小明骑自行车的速度是( )
| A、2.5a m/s |
| B、2.5a |
| C、(2.5+a)m/s |
| D、a÷2.5 |
 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是( )
如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是( )| A、3 | B、6 | C、7 | D、8 |
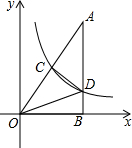 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=