题目内容
(本题满分14分 ,第(1)小题5分,第(2)小题5分,第(3)小题4分)
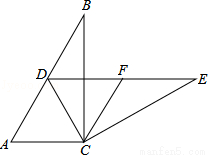
如图,已知在等腰 Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE,



(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当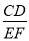 =
=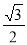 时,求x的值
时,求x的值
(1)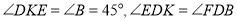 (2)
(2)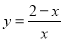 (
(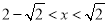 )
)
(3)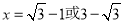
【解析】
试题分析:(1)根据互余的关系可证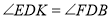 ,利用等腰直角三角形的性质可得
,利用等腰直角三角形的性质可得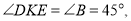 从而可证△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=
从而可证△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=  ,由△DEK∽△DFB可得
,由△DEK∽△DFB可得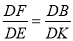 ,所以
,所以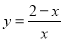 (
(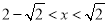 );(3)设CD交EF于点p,EF的中点为Q,连结CQ,根据题意可得
);(3)设CD交EF于点p,EF的中点为Q,连结CQ,根据题意可得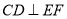 且PC=
且PC=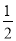 CD,
CD,
CQ=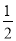 EF,根据
EF,根据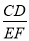 =
=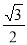 可得
可得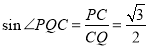 ,所以
,所以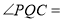 60°,从而∠CFE=∠DFE=30°,所以y=
60°,从而∠CFE=∠DFE=30°,所以y=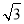 ,所以
,所以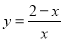 =
=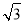 ,然后解方程即可.
,然后解方程即可.
试题解析:(1)根据题意可得∠EDK+∠KDF=90°,∠BDK+∠KDF=90°,所以 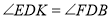 ,又因为△ABC是等腰直角三角形,所以
,又因为△ABC是等腰直角三角形,所以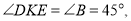 所以△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=
所以△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=  ,由△DEK∽△DFB可得
,由△DEK∽△DFB可得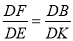 ,所以
,所以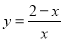 (
(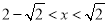 );(3)设CD交EF于点p,EF的中点为Q,连结CQ,由折叠可得
);(3)设CD交EF于点p,EF的中点为Q,连结CQ,由折叠可得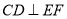 且PC=
且PC=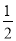 CD,又△CEF是直角三角形,所以CQ=
CD,又△CEF是直角三角形,所以CQ=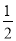 EF,又因为
EF,又因为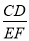 =
=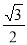 ,所以在Rt△PCQ中有
,所以在Rt△PCQ中有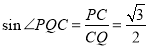 ,所以
,所以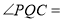 60°,所以∠CFE=∠FCQ=30°,所以∠CFE=∠DFE=30°,所以y=
60°,所以∠CFE=∠FCQ=30°,所以∠CFE=∠DFE=30°,所以y=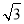 ,所以
,所以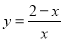 =
=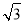 ,解得
,解得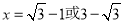 .
.
考点:1. 等腰直角三角形的性质;2.相似三角形的判定与性质;3. 直角三角形的性质;4.图形折叠的性质;5.特殊角的三角函数值;6.函数知识与几何知识的综合.

 名校课堂系列答案
名校课堂系列答案 ∥
∥ ∥
∥ ,
, ,
, ,那么
,那么 的长等于( )
的长等于( )
 ; D.
; D.  ;
;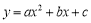
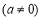 的对称轴为直线
的对称轴为直线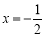 .下列结论中,正确的是( )
.下列结论中,正确的是( )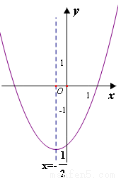
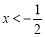 时, y随x的增大而增大
时, y随x的增大而增大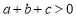
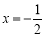 时,y的最小值是
时,y的最小值是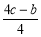
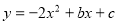 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2). 的开口向上,那么m的取值范围是 .
的开口向上,那么m的取值范围是 .