题目内容
((8分))如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
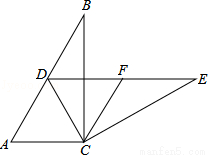
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
(1)60;
(2)四边形ACFD是菱形,理由见解析.
【解析】
试题分析:(1)由已知条件可得△ADC是等边三角形,从而得∠ACD=60°,即为旋转角的度数;
(2)由已知条件可得△DFC是等边三角形,再有(1)中的△ADC是等边三角形,从而可得AD=DF=FC=AC,得四边形ACFD是菱形.
试题解析:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,
∴AC=DC,∠A=60°,
∴△ADC是等边三角形,
∴∠ACD=60°,
∴n的值是60;
(2)四边形ACFD是菱形;
理由:∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形.
考点:1、旋转的性质;2、直角三角形的性质;3、菱形的判定.

练习册系列答案
相关题目
 ,对称轴为直线
,对称轴为直线 ,由此可知这个二次函数的图像一定
,由此可知这个二次函数的图像一定 外的另一点,这点的坐标是 ;
外的另一点,这点的坐标是 ;


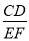 =
=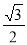 时,求x的值
时,求x的值 的比值是 .
的比值是 . 的图象与一次函数y=﹣x+1的图象在第二象限内的交点坐标(﹣1,n),则k的值是 .
的图象与一次函数y=﹣x+1的图象在第二象限内的交点坐标(﹣1,n),则k的值是 .