题目内容
11.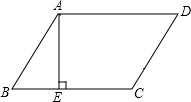 如图,在?ABCD中,∠ADC=60°,DC=4,AE⊥BC,且AE=EC,求平行四边形ABCD的周长和面积.
如图,在?ABCD中,∠ADC=60°,DC=4,AE⊥BC,且AE=EC,求平行四边形ABCD的周长和面积.
分析 由平行四边形的性质可得∠B=∠D=60°,AB=CD=4,由AE⊥BC,可求出AE的长,即平行四边形的高,又AE=CE,可求出BC的长,可求出平行四边形的周长,再利用平行四边形的面积公式即可求出其面积.
解答 解:∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AB=CD=4,
∵AE⊥BC,
∴AE=2$\sqrt{3}$,BE=2,
∵AE=EC,
∴BC=AD=2+2$\sqrt{3}$,
∴平行四边形ABCD的周长=2AB+2BC=8+4+4$\sqrt{3}$=12+4$\sqrt{3}$,
平行四边形ABCD的面积=(2+2$\sqrt{3}$)×$2\sqrt{3}$=4$\sqrt{3}$+12.
点评 此题考查了平行四边形的性质以及直角三角形的性质,解题的关键是利用60°角的锐角三角函数值求出平行四边形的高AE的长.

练习册系列答案
相关题目
 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )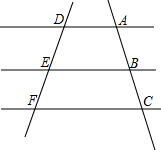 如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.
如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由. 如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).
如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).