题目内容
2.已知关于x的一元二次方程(n+1)(n+2)x2+x-n(n+3)=0的两个实数根分别an,bn(n∈N+),则a1a2…a2009•b1b2…b2009的值是-$\frac{1006}{3015}$.分析 根据根与系数的关系求出an•bn=-$\frac{n(n+3)}{(n+1)(n+2)}$,再把相应的值代入,然后进行约分即可.
解答 解:∵关于x的一元二次方程(n+1)(n+2)x2+x-n(n+3)=0的两个实数根分别an,bn(n∈N+),
∴an•bn=-$\frac{n(n+3)}{(n+1)(n+2)}$,
∴a1a2…a2009•b1b2…b2009=a1b1a2b2…a2009b2009=-$\frac{1×4}{2×3}$×$\frac{2×5}{3×4}$×$\frac{3×6}{4×5}$…×$\frac{2009×2012}{2010×2011}$=-$\frac{1006}{3015}$;
故答案为:-$\frac{1006}{3015}$.
点评 本题考查了根与系数的关系,解题的关键是找出规律,得出anbn=-$\frac{n(n+3)}{(n+1)(n+2)}$.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
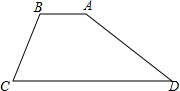 水坝的横截面为梯形ABCD,迎水坡AD的坡角为30°,背水坡BC的坡度为1:1,坝顶宽AB为4m,坝高为6m
水坝的横截面为梯形ABCD,迎水坡AD的坡角为30°,背水坡BC的坡度为1:1,坝顶宽AB为4m,坝高为6m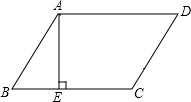 如图,在?ABCD中,∠ADC=60°,DC=4,AE⊥BC,且AE=EC,求平行四边形ABCD的周长和面积.
如图,在?ABCD中,∠ADC=60°,DC=4,AE⊥BC,且AE=EC,求平行四边形ABCD的周长和面积.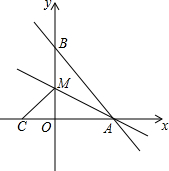 如图,在平面直角坐标系中,直线AB与x,y轴分别交于A,B两点,OB=8,OA=6,M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C
如图,在平面直角坐标系中,直线AB与x,y轴分别交于A,B两点,OB=8,OA=6,M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C