题目内容
5．先化简，再求值：$\frac{{x}^{2}+2x-3}{{x}^{2}+3x-10}$•$\frac{{x}^{2}+8x+15}{1-x}$÷$\frac{{x}^{2}+3x}{2-x}$，其中x=$\frac{1}{3}$．分析 先根据分式的乘除法化简原式，再将x的值代入计算即可得．
解答 解：原式=$\frac{（x-1）（x+3）}{（x-2）（x+5）}$•$\frac{（x+3）（x+5）}{-（x-1）}$•$\frac{-（x-2）}{x（x+3）}$
=x+3，
当x=$\frac{1}{3}$时，原式=3$\frac{1}{3}$．
点评 本题考查了分式的化简求值．解题的关键是对分式的分子分母要因式分解．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
15．下列计算正确的是（ ）
| A． | （-2a）•（-a）=2a2 | B． | 3a2-6a2=-3 | C． | 10a18+2a2=5a5 | D． | -（a3）2=a6 |
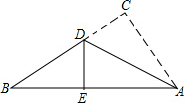如图所示为一张直角三角形纸片，直角边AC=6cm，BC=8cm，小芳将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，你能帮小芳求出CD的长吗？
在△ABC中，DG∥EC，EG∥BC．求证：AE2=AB•AD．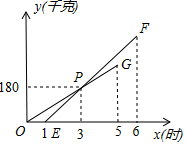
某家装公司聘请两队搬运工来搬运货物，他们都只能连续搬运5小时，甲队于某日0时开始搬运，过了1小时，乙队也开始搬运，如图，线段OG表示甲队搬运量y（千克）与时间x（时）的函数图象，线段EF表示乙队搬运量y（千克）与时间x（时）的函数图象．