Question

13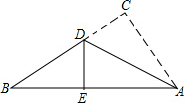．如图所示为一张直角三角形纸片，直角边AC=6cm，BC=8cm，小芳将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，你能帮小芳求出CD的长吗？

Answer 1

分析 首先由勾股定理求得AB=10，然后由翻折求得BE=4，设DC=x，则BD=8-x，在△BDE中，利用勾股定理列方程求解即可．

解答 解：∵AC=6cm，BC=8cm，
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10（cm），
根据折叠可得AC=AE=6cm，
∴BE=AB-AE=10-6=4（cm），
设CD=x，则BD=8-x，DE=x，
在Rt△BDE中，由勾股定理可得x²+4²=（8-x）²，
解得x=3，
∴CD=3cm．

点评 本题主要考查的是翻折变换以及勾股定理的应用，利用翻折的性质和勾股定理表示出△DBE的三边长是解题的关键．