题目内容
当实数a为何取值范围时,下面不等式组恰有两个整数解.
.
|
考点:一元一次不等式组的整数解
专题:
分析:首先解不等式组求得不等式组的解集,然后根据不等式组恰有两个整数解,即可得到一个关于a的不等式组,解得a的范围.
解答:解:
,
解①得:x>-
,
解②得:x<2a,
则不等式组的解集是:-
<x<2a,
不等式有两个整数解,则一定是0和1.
根据题意得:1<2a≤2,
解得:
<x≤1.
|
解①得:x>-
| 2 |
| 5 |
解②得:x<2a,
则不等式组的解集是:-
| 2 |
| 5 |
不等式有两个整数解,则一定是0和1.
根据题意得:1<2a≤2,
解得:
| 1 |
| 2 |
点评:本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
 某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为
某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为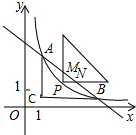 如图,已知反比例函数y=
如图,已知反比例函数y=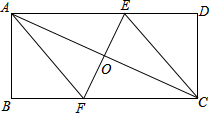 如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O.
如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O.