题目内容
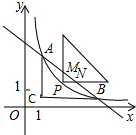 如图,已知反比例函数y=
如图,已知反比例函数y=| 2 |
| x |
| 1 |
| 2 |
(1)求一次函数的解析式;
(2)现有一个直角三角板,让它的直角顶点P在反比例函数图象上的A、B之间的部分滑动(不与A、B重合),两直角边始终分别平行于x轴、y轴,且与线段AB交于M、N两点,试判断P点在滑动过程中,△PMN是否与△CAB总相似,试说明判断理由;
(3)在(2)的条件下,请探究是否存在点P,使得MN:AB=1:3?若存在,求出点P的坐标;若不存在,请说明理由.
考点:反比例函数综合题
专题:综合题
分析:(1)由AC平行于y轴得A点的横坐标为1,根据反比例函数图象上点的坐标特征可确定A点坐标为(1,2),B点坐标为(4,
),然后利用待定系数法求
一次函数解析式;
(2)由于点C的坐标为(1,
),点C的坐标为(1,
),则可判断BC∥x轴,而PM∥y轴,PN∥x轴,所以PN∥BC,PM∥AC,则∠PMN=∠CAB,∠ANM=∠ABC,根据相似三角形的判定即可得到△PMN∽△CAB;
(3)设P点坐标为(a,
),把y=
代入y=-
x+
可得到N点坐标为(5-
,
),则NP=5-
-a,由于△PMN∽△CAB,利用相似比得到5-
-a=1,解得a=2,所以P点坐标为(2,1).
| 1 |
| 2 |
一次函数解析式;
(2)由于点C的坐标为(1,
| 1 |
| 2 |
| 1 |
| 2 |
(3)设P点坐标为(a,
| 2 |
| a |
| 2 |
| a |
| 1 |
| 2 |
| 5 |
| 2 |
| 4 |
| a |
| 2 |
| a |
| 4 |
| a |
| 4 |
| a |
解答:解:(1)∵点C的坐标为(1,
),AC平行于y轴,
∴A点的横坐标为1,
把x=1代入y=
得y=2,
∴A点坐标为(1,2),
把x=4代入y=
得y=
,
∴B点坐标为(4,
),
把A(1,2),B(4,
)代入y=kx+b得
,解得
,
∴一次函数解析式为y=-
x+
;
(2)△PMN与△CAB总相似.理由如下:
∵点C的坐标为(1,
),点C的坐标为(1,
),
∴BC∥x轴,
∵PM∥y轴,PN∥x轴,
∴PN∥BC,PM∥AC,
∴∠PMN=∠CAB,∠ANM=∠ABC,
∴△PMN∽△CAB;
(3)存在.
设P点坐标为(a,
),
把y=
代入y=-
x+
得-
x+
=
,即得x=5-
,
∴N点坐标为(5-
,
),
∴NP=5-
-a,
∵△PMN∽△CAB,
∴
=
,
而MN:AB=1:3,BC=3,
∴5-
-a=1,
整理得a2-4a+4=0,解得a1=a2=2,
∴P点坐标为(2,1).
| 1 |
| 2 |
∴A点的横坐标为1,
把x=1代入y=
| 2 |
| x |
∴A点坐标为(1,2),
把x=4代入y=
| 2 |
| x |
| 1 |
| 2 |
∴B点坐标为(4,
| 1 |
| 2 |
把A(1,2),B(4,
| 1 |
| 2 |
|
|
∴一次函数解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)△PMN与△CAB总相似.理由如下:
∵点C的坐标为(1,
| 1 |
| 2 |
| 1 |
| 2 |
∴BC∥x轴,
∵PM∥y轴,PN∥x轴,
∴PN∥BC,PM∥AC,
∴∠PMN=∠CAB,∠ANM=∠ABC,
∴△PMN∽△CAB;
(3)存在.
设P点坐标为(a,
| 2 |
| a |
把y=
| 2 |
| a |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
| a |
| 4 |
| a |
∴N点坐标为(5-
| 4 |
| a |
| 2 |
| a |
∴NP=5-
| 4 |
| a |
∵△PMN∽△CAB,
∴
| MN |
| AB |
| NP |
| BC |
而MN:AB=1:3,BC=3,
∴5-
| 4 |
| a |
整理得a2-4a+4=0,解得a1=a2=2,
∴P点坐标为(2,1).
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、图形与坐标的关系和相似三角形的判定与性质;会运用待定系数法求函数的解析式.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
下面化简正确的是( )
| A、2x-5xy=-3y | ||||
B、
| ||||
| C、(2x+1)2=4x2+1 | ||||
D、若x>0,
|
 调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为
调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为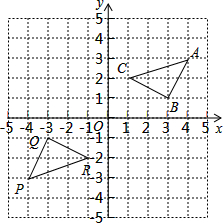 如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
 张华同学家要建一个长方形的养鸡场,鸡场的一边靠墙(墙长为25米),另三边用长40米的竹篱笆围成.问长方形的鸡场的面积能否达到128m2?如果能,AB的长是多少米?如果不能,请说明理由.
张华同学家要建一个长方形的养鸡场,鸡场的一边靠墙(墙长为25米),另三边用长40米的竹篱笆围成.问长方形的鸡场的面积能否达到128m2?如果能,AB的长是多少米?如果不能,请说明理由. 如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.
如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.