题目内容
 某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为
某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为考点:二次函数的应用
专题:
分析:由函数的图象可知点(30,2700)和点(60,0)满足解析式w=mx2+n,设销售量为a,代入函数的解析式,即可得到a和x的关系.
解答:解:由函数的图象可知点(30,2700)和点(60,0)满足解析式w=mx2+n,
∴
,
解得:
,
∴w=-x2+3600,
设销售量为a,则a(60-x)=w,
即a(60-x)=-x2+3600,
解得:a=(60+x ),
故答案为:(60+x).
∴
|
解得:
|
∴w=-x2+3600,
设销售量为a,则a(60-x)=w,
即a(60-x)=-x2+3600,
解得:a=(60+x ),
故答案为:(60+x).
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题,用的知识点为:因式分解,题目设计比较新颖,同时也考查了学生的逆向思维思考问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
下面化简正确的是( )
| A、2x-5xy=-3y | ||||
B、
| ||||
| C、(2x+1)2=4x2+1 | ||||
D、若x>0,
|
 如图,四边形ABCD是矩形,把矩形沿直线BD折叠,点C落在点E处,连接BE,与AD交于点M.
如图,四边形ABCD是矩形,把矩形沿直线BD折叠,点C落在点E处,连接BE,与AD交于点M. 调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为
调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为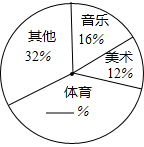 为了解某区初三学生的课余生活情况,调查小组在全区范围内随机抽取部分学生进行问卷调查.问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图(如图).如果该区有6000名初三学生,请你估计该区最喜欢体育运动的初三学生约有
为了解某区初三学生的课余生活情况,调查小组在全区范围内随机抽取部分学生进行问卷调查.问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图(如图).如果该区有6000名初三学生,请你估计该区最喜欢体育运动的初三学生约有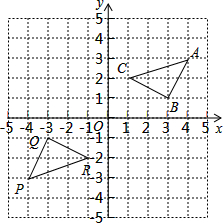 如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?