题目内容
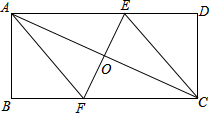 如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O.
如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F、E,垂足为O.(1)求证:四边形AFCE为菱形;
(2)若AB=4,BC=8,求菱形AFCE的面积.
考点:菱形的判定与性质,线段垂直平分线的性质,矩形的性质
专题:
分析:(1)先证明△AOE≌△COF,得出OE=OF,再根据EF垂直平分AC,可得出四边形AFCE为菱形;
(2)设AF=x,由AB=4,BC=8,得BF=8-x,根据勾股定理可得出AF的长,根据菱形的面积求解即可.
(2)设AF=x,由AB=4,BC=8,得BF=8-x,根据勾股定理可得出AF的长,根据菱形的面积求解即可.
解答:解:(1)证明:∵EF垂直平分AC,
∴OA=OC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EAO=∠FOC,AOE=∠COF,
∴在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为菱形;(6分)
(2)设AF=x,
∵AB=4,BC=8,∴BF=8-x,
∴AF2=AB2+BF2,
∴x2=42+(8-x)2,
∴x=5,
∴S菱形AFCE=FC•AB=5×4=20,
∴菱形面积为20.(2分)
∴OA=OC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EAO=∠FOC,AOE=∠COF,
∴在△AOE和△COF中,
|
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为菱形;(6分)
(2)设AF=x,
∵AB=4,BC=8,∴BF=8-x,
∴AF2=AB2+BF2,
∴x2=42+(8-x)2,
∴x=5,
∴S菱形AFCE=FC•AB=5×4=20,
∴菱形面积为20.(2分)
点评:本题考查了菱形的性质、线段垂直平分线的性质、矩形的性质以及面积的求法,是重点知识,要熟练掌握.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
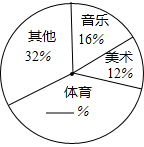 为了解某区初三学生的课余生活情况,调查小组在全区范围内随机抽取部分学生进行问卷调查.问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图(如图).如果该区有6000名初三学生,请你估计该区最喜欢体育运动的初三学生约有
为了解某区初三学生的课余生活情况,调查小组在全区范围内随机抽取部分学生进行问卷调查.问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图(如图).如果该区有6000名初三学生,请你估计该区最喜欢体育运动的初三学生约有 张华同学家要建一个长方形的养鸡场,鸡场的一边靠墙(墙长为25米),另三边用长40米的竹篱笆围成.问长方形的鸡场的面积能否达到128m2?如果能,AB的长是多少米?如果不能,请说明理由.
张华同学家要建一个长方形的养鸡场,鸡场的一边靠墙(墙长为25米),另三边用长40米的竹篱笆围成.问长方形的鸡场的面积能否达到128m2?如果能,AB的长是多少米?如果不能,请说明理由.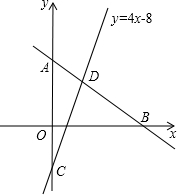 如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线y=4x-8与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积.
如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线y=4x-8与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积.