题目内容
8. 一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )
一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )| A. | m>-1 | B. | m<-2 | C. | -2<m<-1 | D. | m<-1 |
分析 根据图象在坐标平面内的位置关系知m+2<0且1-m<0,据此可以求得m的取值范围.
解答 解:如图所示,y=(m+2)x+(1-m)的图象经过第二、三、四象限,
∴$\left\{\begin{array}{l}{m+2<0}\\{1+m<0}\end{array}\right.$,
解得m<-2.
故选B.
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
相关题目
20.当x=2时,多项式mx3-x+5m+3的值是118,则多项式m2-6m-7的值为( )
| A. | -16 | B. | -7 | C. | 20 | D. | 93 |
16.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 正三角形 | D. | 圆 |
17.我市农业结构调整取得了巨大成功,今年水果又喜获丰收,某果园组织30辆汽车装运A、B、C三种水果共84t到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆;同时,装运的B种水果的汽车辆数不超过装运的A、C两种水果的汽车辆数之和.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
(2)设此次外销活动的利润为Q(百元),求Q与x之间的函数关系式,请你提出一个获得最大利润时的车辆分配方案.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
 是同类二次根式的是( )
是同类二次根式的是( ) B.
B.  C.
C.  D.
D. 
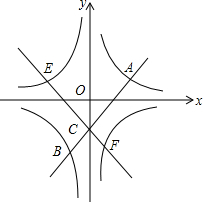 如图,在平面直角坐标系中,双曲线y=$\frac{1}{x}$与一次函数y=kx+b(k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线.若新直线与双曲线y=-$\frac{1}{x}$相交于点E、F,并使得双曲线y=$\frac{1}{x}$,y=-$\frac{1}{x}$,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小.最小值是多少?
如图,在平面直角坐标系中,双曲线y=$\frac{1}{x}$与一次函数y=kx+b(k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线.若新直线与双曲线y=-$\frac{1}{x}$相交于点E、F,并使得双曲线y=$\frac{1}{x}$,y=-$\frac{1}{x}$,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小.最小值是多少?
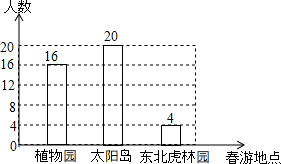 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.