题目内容
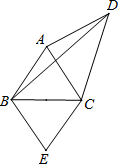 如图,AB=AC=AD=BE=CE,∠E=70°,则∠BDC的大小是( )
如图,AB=AC=AD=BE=CE,∠E=70°,则∠BDC的大小是( )| A、20° | B、30° |
| C、25° | D、35° |
考点:圆周角定理,菱形的判定与性质
专题:
分析:先根据AB=AC=BE=CE可知四边形ABEC是菱形,故∠E=∠BAC=70°,再根据AB=AC=AD可知B、C、D三点在以点A为圆心,以AD的长为半径的圆周上,由圆周角定理即可得出结论.
解答:解:∵AB=AC=BE=CE,
∴四边形ABEC是菱形,
∴∠E=∠BAC=70°,
∵AB=AC=AD,
∴B、C、D三点在以点A为圆心,以AD的长为半径的圆周上,
∴∠BDC=
∠BAC=
×70°=35°.
故选D.
∴四边形ABEC是菱形,
∴∠E=∠BAC=70°,
∵AB=AC=AD,
∴B、C、D三点在以点A为圆心,以AD的长为半径的圆周上,
∴∠BDC=
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
已知实数a,b,c,并且
=
=
=k,则直线y=kx-3一定通过( )
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| A、第一、二、三象限 |
| B、第三、四象限 |
| C、第一、三、四象限 |
| D、第一、二象限 |
若a2=25,b2=36,且ab<0,则a-b的值为( )
| A、-1或11 | B、-1或-11 |
| C、±1 | D、±11 |
 如图,在房间内,有一梯子MC斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角∠ACM是75°,如果梯子底端C不动,顶端靠在对面的墙上,此时梯子顶端距地面的距离NB为b米,梯子的倾斜角∠BCN为45°,这间房子的宽AB是
如图,在房间内,有一梯子MC斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角∠ACM是75°,如果梯子底端C不动,顶端靠在对面的墙上,此时梯子顶端距地面的距离NB为b米,梯子的倾斜角∠BCN为45°,这间房子的宽AB是