题目内容
1.已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+3y+1=0}\\{3x-2y+2=0}\end{array}\right.$的解,则不等式ax-b+1>0的解是( )| A. | x$<\frac{3}{2}$ | B. | x$<-\frac{3}{2}$ | C. | x$>\frac{3}{2}$ | D. | x$>-\frac{3}{2}$ |
分析 把方程组的解代入方程组,求出a、b的值,代入解不等式即可.
解答 解:∵$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+3y+1=0}\\{3x-2y+2=0}\end{array}\right.$的解,
∴代入得:$\left\{\begin{array}{l}{2a+3b=-1}\\{3a-2b=-2}\end{array}\right.$,
解得:a=-$\frac{8}{13}$,b=$\frac{1}{13}$,
∴ax-b+1>0,
∴-$\frac{8}{13}$x-$\frac{1}{13}$+1>0,
解得:x<$\frac{3}{2}$,
故选A.
点评 本题考查了二元一次方程组的解,解一元一次不等式的应用,能求出a、b的值是解此题的关键.

练习册系列答案
相关题目
6.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
| A. | x2+9=0 | B. | 4x2-4x+1=0 | C. | x2+x+1=0 | D. | x2+x-1=0 |
 正方形ABCD中,F为DC中点,E为BC上一点,且EC=$\frac{1}{4}$BC.
正方形ABCD中,F为DC中点,E为BC上一点,且EC=$\frac{1}{4}$BC.
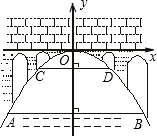 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.